NEET-XII-Physics
31: Capacitors
- #25Find the potential difference
Va-Vbbetween the points a and b shown in each part of the figure (31-E14).
Figure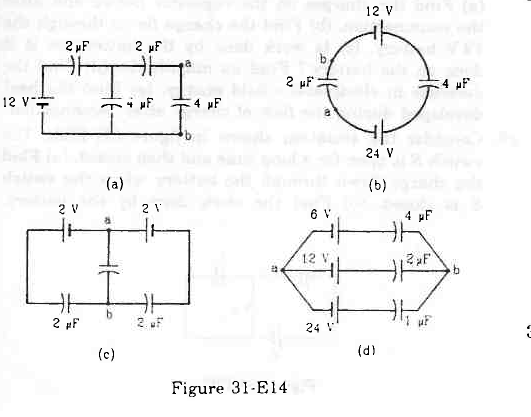
Ans : (a) `` q={q}_{1}+{q}_{2}`` ...(i)
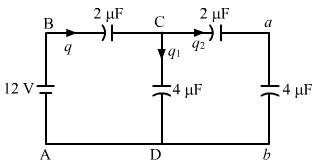
On applying Kirchhoff's voltage law in the loop CabDC, we get
`` \frac{{q}_{2}}{2}+\frac{{q}_{2}}{4}-\frac{{q}_{1}}{4}=0``
`` \Rightarrow 2{q}_{2}+{q}_{2}-{q}_{1}=0``
`` \Rightarrow 3{q}_{2}={q}_{1}...\left(\,\mathrm{\,ii\,}\right)``
On applying Kirchhoff's voltage law in the loop DCBAD, we get
`` \frac{q}{2}+\frac{{q}_{1}}{4}-12=0``
`` \Rightarrow \frac{{q}_{1}+{q}_{2}}{2}+\frac{{q}_{1}}{4}-12=0``
`` \Rightarrow 3{q}_{1}+2{q}_{2}=48...\left(\,\mathrm{\,iii\,}\right)``
From eqs. (ii) and (iii), we get
`` 9{q}_{2}+2{q}_{2}=48``
`` \Rightarrow 11{q}_{2}=48``
`` \Rightarrow {q}_{2}=\frac{48}{11}``
`` \,\mathrm{\,Now\,},``
`` {\,\mathrm{\,V\,}}_{a}-{\,\mathrm{\,V\,}}_{b}=\frac{{q}_{2}}{4\,\mathrm{\,\mu F\,}}=\frac{48}{44}=\frac{12}{11}\,\mathrm{\,V\,}``
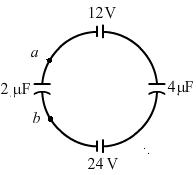
(b) Let the charge in the loop be q.
Now, on applying Kirchhoff's voltage law in the loop, we get
`` \frac{q}{2}+\frac{q}{4}-24+12=0``
`` \Rightarrow \frac{3q}{4}=12``
`` \Rightarrow q=16\,\mathrm{\,\mu C\,}``
`` \,\mathrm{\,Now\,},``
`` {V}_{a}-{V}_{b}=\frac{-q}{2\,\mathrm{\,\mu F\,}}``
`` \Rightarrow {V}_{a}-{V}_{b}=\frac{-16\,\mathrm{\,\mu C\,}}{2\,\mathrm{\,\mu F\,}}=-8\,\mathrm{\,V\,}``
(c) `` {V}_{\,\mathrm{\,a\,}}-{V}_{\,\mathrm{\,b\,}}=2-\frac{2-q}{2\,\mathrm{\,\mu F\,}}``
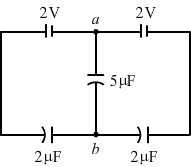
In the loop,
`` 2+2-\frac{q}{2}-\frac{q}{2}=0``
`` \Rightarrow q=4\,\mathrm{\,C\,}``
`` \therefore {V}_{\,\mathrm{\,a\,}}-{V}_{\,\mathrm{\,b\,}}=2-\frac{4}{2}=2-2=0\,\mathrm{\,V\,}``
(d)
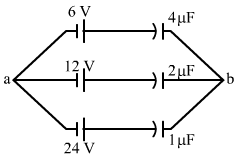
Net charge flowing through all branches, q = 24 + 24 + 24 = 72 μC
Net capacitance of all branches, C = 4 + 2 + 1 = 7 μF
The total potential difference (V) between points a and b is given by
`` V=\frac{q}{C}``
`` \Rightarrow V=\frac{72}{7}=10.3\,\mathrm{\,V\,}``
As the negative terminals of the batteries are connected to a, the net potential between points a and b is `` -``10.3 V.
Page No 167: