HomeLearn Fast select Course
Show Unit/ChapterChange UnitChange SubjectLast Menu
NEET-XII-Physics

31: Capacitors

with Solutions - page 4
Qstn# iv-24-a Prvs-QstnNext-Qstn
  • #24-a
    , (b) and (c) figure (31-E13) are identical. Find the capacitance between the points A and B of the assembly.
    FigureA B (b) and (c) figure (31-E13) are identical. Find the capacitance between the points A and B of the assembly.
    FigureA B
    Ans : , (b) and (c) are identical, as all of them form a bridge circuit. In that circuit, capacitors of 1 µF and 2 µF are connected to terminal A and the 5 µF capacitor and capacitors of 3 µF and 6 µF are connected to terminal B and the 5 µF capacitor.
    For the given situation, it can be observed that the bridge is in balance; thus, no current will flow through the 5 µF capacitor.
    So to simplify the circuit, 5 µF capacitor can be removed from the circuit.
    Now, 1 µF and 3 µF capacitors are in series.
    And 2 µF and 6 µF capacitors are also in series combination.
    These two combination are in parallel with each other.
    The equivalent capacitance can be calculated as:
    `` {C}_{\,\mathrm{\,eq\,}}=\frac{1\times 3}{1+3}+\frac{2\times 6}{2+6}``
    `` =\frac{3}{4}+\frac{12}{8}=\frac{9}{4}\,\mathrm{\,\mu F\,}=2.25\mu F``
    ∴ Ceq = 2.25 µF
    Thus, parts
    (a),
    (b) and
    (c) are identical.
    And,
    Ceq = 2.25 µF
    Page No 167: (b) and (c) are identical, as all of them form a bridge circuit. In that circuit, capacitors of 1 µF and 2 µF are connected to terminal A and the 5 µF capacitor and capacitors of 3 µF and 6 µF are connected to terminal B and the 5 µF capacitor.
    For the given situation, it can be observed that the bridge is in balance; thus, no current will flow through the 5 µF capacitor.
    So to simplify the circuit, 5 µF capacitor can be removed from the circuit.
    Now, 1 µF and 3 µF capacitors are in series.
    And 2 µF and 6 µF capacitors are also in series combination.
    These two combination are in parallel with each other.
    The equivalent capacitance can be calculated as:
    `` {C}_{\,\mathrm{\,eq\,}}=\frac{1\times 3}{1+3}+\frac{2\times 6}{2+6}``
    `` =\frac{3}{4}+\frac{12}{8}=\frac{9}{4}\,\mathrm{\,\mu F\,}=2.25\mu F``
    ∴ Ceq = 2.25 µF
    Thus, parts
    (a),
    (b) and
    (c) are identical.
    And,
    Ceq = 2.25 µF
    Page No 167:
  • #24-b
    and
    Ans : and
  • #24-c
    figure (31-E13) are identical. Find the capacitance between the points A and B of the assembly.
    FigureA B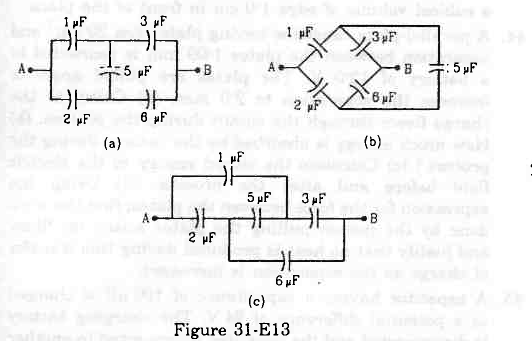
    Ans : are identical, as all of them form a bridge circuit. In that circuit, capacitors of 1 µF and 2 µF are connected to terminal A and the 5 µF capacitor and capacitors of 3 µF and 6 µF are connected to terminal B and the 5 µF capacitor.
    For the given situation, it can be observed that the bridge is in balance; thus, no current will flow through the 5 µF capacitor.
    So to simplify the circuit, 5 µF capacitor can be removed from the circuit.
    Now, 1 µF and 3 µF capacitors are in series.
    And 2 µF and 6 µF capacitors are also in series combination.
    These two combination are in parallel with each other.
    The equivalent capacitance can be calculated as:
    `` {C}_{\,\mathrm{\,eq\,}}=\frac{1\times 3}{1+3}+\frac{2\times 6}{2+6}``
    `` =\frac{3}{4}+\frac{12}{8}=\frac{9}{4}\,\mathrm{\,\mu F\,}=2.25\mu F``
    ∴ Ceq = 2.25 µF
    Thus, parts
    (a),
    (b) and
    (c) are identical.
    And,
    Ceq = 2.25 µF
    Page No 167: