NEET-XII-Physics
28: Heat Transfer
- #30The three rods shown in figure (28-E7) have identical geometrical dimensions. Heat flows from the hot end at a rate of 40 W in the arrangement (a) Find the rates of heat flow when the rods are joined as in arrangement (b) and in (c) Thermal condcutivities of aluminium and copper are 200 W m-1°C-1 and 400 W m-1°C-1 respectively.
Figure (a) Find the rates of heat flow when the rods are joined as in arrangement (b) and in (c) Thermal condcutivities of aluminium and copper are 200 W m-1°C-1 and 400 W m-1°C-1 respectively.
Figure Ans : For arrangement (a) ,
Ans : For arrangement (a) ,
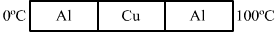
Temperature of the hot end ,T1 = 100°C
Temperature of the cold end ,T2 = 0°C
Rs = R1 + R2 + R3
`` =\frac{l}{{K}_{\,\mathrm{\,Al\,}}\,\mathrm{\,A\,}}+\frac{l}{{K}_{\,\mathrm{\,cu\,}}\,\mathrm{\,A\,}}+\frac{l}{{K}_{\mathit{Al}}A}``
`` =\frac{\mathit{l}}{\mathit{A}}\left(\frac{1}{200}+\frac{1}{400}+\frac{1}{200}\right)``
`` =\frac{l}{\,\mathrm{\,A\,}}\left(\frac{5}{400}\right)``
`` =\frac{l}{\,\mathrm{\,A\,}}\times \frac{1}{80}``
`` \frac{\,\mathrm{\,d\,}Q}{dt}=q=\,\mathrm{\,Rate\,}\,\mathrm{\,of\,}\,\mathrm{\,flow\,}\,\mathrm{\,of\,}\,\mathrm{\,heat\,}=\frac{{T}_{1}-{T}_{2}}{{R}_{\,\mathrm{\,S\,}}}``
`` =\frac{100-0}{{\displaystyle \frac{l}{\,\mathrm{\,A\,}}\times \frac{1}{80}}}``
`` ``
`` \,\mathrm{\,Given\,}:``
`` q=40\,\mathrm{\,W\,}``
`` 40=\frac{100}{{\displaystyle \frac{l}{\,\mathrm{\,A\,}}}\times {\displaystyle \frac{1}{80}}}``
`` \Rightarrow \frac{l}{\,\mathrm{\,A\,}}=200``
`` \Rightarrow \frac{\,\mathrm{\,A\,}}{l}=\frac{1}{200}``
`` ``
For arrangement (b) ,
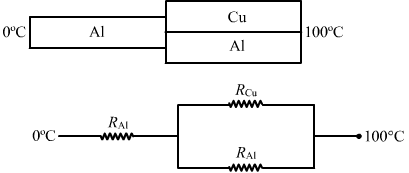
`` {R}_{\,\mathrm{\,net\,}}={R}_{\,\mathrm{\,Al\,}}+\frac{{R}_{\,\mathrm{\,Cu\,}}\times {R}_{\,\mathrm{\,Al\,}}}{{\,\mathrm{\,R\,}}_{\,\mathrm{\,Cu\,}}+{\,\mathrm{\,R\,}}_{\,\mathrm{\,Al\,}}}``
`` =\frac{l}{{K}_{\,\mathrm{\,Al\,}}A}+\frac{{\displaystyle \frac{l}{{K}_{\,\mathrm{\,Cu\,}}A}}\times {\displaystyle \frac{l}{{K}_{\,\mathrm{\,Al\,}}l}}}{{\displaystyle \frac{l}{{K}_{\,\mathrm{\,Cu\,}}A}}+{\displaystyle \frac{l}{{K}_{\mathit{Al}}\,\mathrm{\,A\,}}}}``
`` =\frac{\mathit{l}}{\mathit{A}\mathit{·}{\mathit{K}}_{\mathit{Al}}}\mathit{+}\frac{\mathit{l}}{\mathit{A}\left({\mathit{K}}_{\mathit{Al}}\mathit{+}{\mathit{K}}_{\mathit{Cu}}\right)}``
`` =\frac{l}{\,\mathrm{\,A\,}}\left(\frac{1}{200}+\frac{1}{200+400}\right)``
`` =\frac{l}{\,\mathrm{\,A\,}}\left(\frac{1}{200}+\frac{1}{600}\right)``
`` =\frac{4}{600}.\frac{l}{\,\mathrm{\,A\,}}``
Rate of flow of heat is given by
`` q=\frac{{\,\mathrm{\,T\,}}_{1}-{\,\mathrm{\,T\,}}_{2}}{{\,\mathrm{\,R\,}}_{\,\mathrm{\,net\,}}}``
`` =\frac{\left(100-0\right)}{4l}600\,\mathrm{\,A\,}``
`` =\frac{100\times 600}{4}\times \frac{1}{200}``
`` =75\,\mathrm{\,W\,}``
For arrangement (c) ,
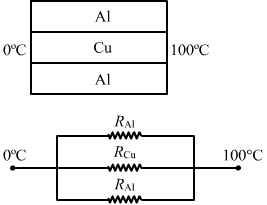
`` \frac{\mathit{1}}{{\mathit{R}}_{\mathit{net}}}\mathit{=}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{Al}}}\mathit{+}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{Cu}}}\mathit{+}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{Al}}}``
`` =\frac{{K}_{\,\mathrm{\,Al\,}}A}{l}+\frac{{K}_{\,\mathrm{\,Cu\,}}A}{l}+\frac{{K}_{\,\mathrm{\,Al\,}}A}{l}``
`` \frac{1}{{R}_{\,\mathrm{\,net\,}}}=\left({K}_{\,\mathrm{\,Al\,}}+{K}_{\,\mathrm{\,Cu\,}}+{K}_{\,\mathrm{\,Al\,}}\right)\frac{\mathit{A}}{\mathit{l}}``
`` \frac{1}{{R}_{\,\mathrm{\,net\,}}}=\left(200+400+200\right)\times \frac{1}{200}``
`` \Rightarrow {R}_{\,\mathrm{\,net\,}}=\frac{200}{800}``
`` =\frac{1}{4}``
`` ``
`` \,\mathrm{\,Rate\,}\,\mathrm{\,of\,}\,\mathrm{\,heat\,}\,\mathrm{\,flow\,}=\frac{\Delta T}{{R}_{\,\mathrm{\,net\,}}}``
`` =\frac{100}{{\displaystyle \frac{1}{4}}}``
`` =400\,\mathrm{\,W\,}``
Page No 100: (a) ,
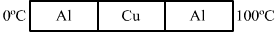
Temperature of the hot end ,T1 = 100°C
Temperature of the cold end ,T2 = 0°C
Rs = R1 + R2 + R3
`` =\frac{l}{{K}_{\,\mathrm{\,Al\,}}\,\mathrm{\,A\,}}+\frac{l}{{K}_{\,\mathrm{\,cu\,}}\,\mathrm{\,A\,}}+\frac{l}{{K}_{\mathit{Al}}A}``
`` =\frac{\mathit{l}}{\mathit{A}}\left(\frac{1}{200}+\frac{1}{400}+\frac{1}{200}\right)``
`` =\frac{l}{\,\mathrm{\,A\,}}\left(\frac{5}{400}\right)``
`` =\frac{l}{\,\mathrm{\,A\,}}\times \frac{1}{80}``
`` \frac{\,\mathrm{\,d\,}Q}{dt}=q=\,\mathrm{\,Rate\,}\,\mathrm{\,of\,}\,\mathrm{\,flow\,}\,\mathrm{\,of\,}\,\mathrm{\,heat\,}=\frac{{T}_{1}-{T}_{2}}{{R}_{\,\mathrm{\,S\,}}}``
`` =\frac{100-0}{{\displaystyle \frac{l}{\,\mathrm{\,A\,}}\times \frac{1}{80}}}``
`` ``
`` \,\mathrm{\,Given\,}:``
`` q=40\,\mathrm{\,W\,}``
`` 40=\frac{100}{{\displaystyle \frac{l}{\,\mathrm{\,A\,}}}\times {\displaystyle \frac{1}{80}}}``
`` \Rightarrow \frac{l}{\,\mathrm{\,A\,}}=200``
`` \Rightarrow \frac{\,\mathrm{\,A\,}}{l}=\frac{1}{200}``
`` ``
For arrangement (b) ,

`` {R}_{\,\mathrm{\,net\,}}={R}_{\,\mathrm{\,Al\,}}+\frac{{R}_{\,\mathrm{\,Cu\,}}\times {R}_{\,\mathrm{\,Al\,}}}{{\,\mathrm{\,R\,}}_{\,\mathrm{\,Cu\,}}+{\,\mathrm{\,R\,}}_{\,\mathrm{\,Al\,}}}``
`` =\frac{l}{{K}_{\,\mathrm{\,Al\,}}A}+\frac{{\displaystyle \frac{l}{{K}_{\,\mathrm{\,Cu\,}}A}}\times {\displaystyle \frac{l}{{K}_{\,\mathrm{\,Al\,}}l}}}{{\displaystyle \frac{l}{{K}_{\,\mathrm{\,Cu\,}}A}}+{\displaystyle \frac{l}{{K}_{\mathit{Al}}\,\mathrm{\,A\,}}}}``
`` =\frac{\mathit{l}}{\mathit{A}\mathit{·}{\mathit{K}}_{\mathit{Al}}}\mathit{+}\frac{\mathit{l}}{\mathit{A}\left({\mathit{K}}_{\mathit{Al}}\mathit{+}{\mathit{K}}_{\mathit{Cu}}\right)}``
`` =\frac{l}{\,\mathrm{\,A\,}}\left(\frac{1}{200}+\frac{1}{200+400}\right)``
`` =\frac{l}{\,\mathrm{\,A\,}}\left(\frac{1}{200}+\frac{1}{600}\right)``
`` =\frac{4}{600}.\frac{l}{\,\mathrm{\,A\,}}``
Rate of flow of heat is given by
`` q=\frac{{\,\mathrm{\,T\,}}_{1}-{\,\mathrm{\,T\,}}_{2}}{{\,\mathrm{\,R\,}}_{\,\mathrm{\,net\,}}}``
`` =\frac{\left(100-0\right)}{4l}600\,\mathrm{\,A\,}``
`` =\frac{100\times 600}{4}\times \frac{1}{200}``
`` =75\,\mathrm{\,W\,}``
For arrangement (c) ,

`` \frac{\mathit{1}}{{\mathit{R}}_{\mathit{net}}}\mathit{=}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{Al}}}\mathit{+}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{Cu}}}\mathit{+}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{Al}}}``
`` =\frac{{K}_{\,\mathrm{\,Al\,}}A}{l}+\frac{{K}_{\,\mathrm{\,Cu\,}}A}{l}+\frac{{K}_{\,\mathrm{\,Al\,}}A}{l}``
`` \frac{1}{{R}_{\,\mathrm{\,net\,}}}=\left({K}_{\,\mathrm{\,Al\,}}+{K}_{\,\mathrm{\,Cu\,}}+{K}_{\,\mathrm{\,Al\,}}\right)\frac{\mathit{A}}{\mathit{l}}``
`` \frac{1}{{R}_{\,\mathrm{\,net\,}}}=\left(200+400+200\right)\times \frac{1}{200}``
`` \Rightarrow {R}_{\,\mathrm{\,net\,}}=\frac{200}{800}``
`` =\frac{1}{4}``
`` ``
`` \,\mathrm{\,Rate\,}\,\mathrm{\,of\,}\,\mathrm{\,heat\,}\,\mathrm{\,flow\,}=\frac{\Delta T}{{R}_{\,\mathrm{\,net\,}}}``
`` =\frac{100}{{\displaystyle \frac{1}{4}}}``
`` =400\,\mathrm{\,W\,}``
Page No 100:
- #30-aFind the rates of heat flow when the rods are joined as in arrangementAns : ,
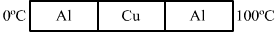
Temperature of the hot end ,T1 = 100°C
Temperature of the cold end ,T2 = 0°C
Rs = R1 + R2 + R3
`` =\frac{l}{{K}_{\,\mathrm{\,Al\,}}\,\mathrm{\,A\,}}+\frac{l}{{K}_{\,\mathrm{\,cu\,}}\,\mathrm{\,A\,}}+\frac{l}{{K}_{\mathit{Al}}A}``
`` =\frac{\mathit{l}}{\mathit{A}}\left(\frac{1}{200}+\frac{1}{400}+\frac{1}{200}\right)``
`` =\frac{l}{\,\mathrm{\,A\,}}\left(\frac{5}{400}\right)``
`` =\frac{l}{\,\mathrm{\,A\,}}\times \frac{1}{80}``
`` \frac{\,\mathrm{\,d\,}Q}{dt}=q=\,\mathrm{\,Rate\,}\,\mathrm{\,of\,}\,\mathrm{\,flow\,}\,\mathrm{\,of\,}\,\mathrm{\,heat\,}=\frac{{T}_{1}-{T}_{2}}{{R}_{\,\mathrm{\,S\,}}}``
`` =\frac{100-0}{{\displaystyle \frac{l}{\,\mathrm{\,A\,}}\times \frac{1}{80}}}``
`` ``
`` \,\mathrm{\,Given\,}:``
`` q=40\,\mathrm{\,W\,}``
`` 40=\frac{100}{{\displaystyle \frac{l}{\,\mathrm{\,A\,}}}\times {\displaystyle \frac{1}{80}}}``
`` \Rightarrow \frac{l}{\,\mathrm{\,A\,}}=200``
`` \Rightarrow \frac{\,\mathrm{\,A\,}}{l}=\frac{1}{200}``
`` ``
For arrangement
- #30-band inAns : ,

`` {R}_{\,\mathrm{\,net\,}}={R}_{\,\mathrm{\,Al\,}}+\frac{{R}_{\,\mathrm{\,Cu\,}}\times {R}_{\,\mathrm{\,Al\,}}}{{\,\mathrm{\,R\,}}_{\,\mathrm{\,Cu\,}}+{\,\mathrm{\,R\,}}_{\,\mathrm{\,Al\,}}}``
`` =\frac{l}{{K}_{\,\mathrm{\,Al\,}}A}+\frac{{\displaystyle \frac{l}{{K}_{\,\mathrm{\,Cu\,}}A}}\times {\displaystyle \frac{l}{{K}_{\,\mathrm{\,Al\,}}l}}}{{\displaystyle \frac{l}{{K}_{\,\mathrm{\,Cu\,}}A}}+{\displaystyle \frac{l}{{K}_{\mathit{Al}}\,\mathrm{\,A\,}}}}``
`` =\frac{\mathit{l}}{\mathit{A}\mathit{·}{\mathit{K}}_{\mathit{Al}}}\mathit{+}\frac{\mathit{l}}{\mathit{A}\left({\mathit{K}}_{\mathit{Al}}\mathit{+}{\mathit{K}}_{\mathit{Cu}}\right)}``
`` =\frac{l}{\,\mathrm{\,A\,}}\left(\frac{1}{200}+\frac{1}{200+400}\right)``
`` =\frac{l}{\,\mathrm{\,A\,}}\left(\frac{1}{200}+\frac{1}{600}\right)``
`` =\frac{4}{600}.\frac{l}{\,\mathrm{\,A\,}}``
Rate of flow of heat is given by
`` q=\frac{{\,\mathrm{\,T\,}}_{1}-{\,\mathrm{\,T\,}}_{2}}{{\,\mathrm{\,R\,}}_{\,\mathrm{\,net\,}}}``
`` =\frac{\left(100-0\right)}{4l}600\,\mathrm{\,A\,}``
`` =\frac{100\times 600}{4}\times \frac{1}{200}``
`` =75\,\mathrm{\,W\,}``
For arrangement
- #30-cThermal condcutivities of aluminium and copper are 200 W m-1°C-1 and 400 W m-1°C-1 respectively.
FigureAns : ,

`` \frac{\mathit{1}}{{\mathit{R}}_{\mathit{net}}}\mathit{=}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{Al}}}\mathit{+}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{Cu}}}\mathit{+}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{Al}}}``
`` =\frac{{K}_{\,\mathrm{\,Al\,}}A}{l}+\frac{{K}_{\,\mathrm{\,Cu\,}}A}{l}+\frac{{K}_{\,\mathrm{\,Al\,}}A}{l}``
`` \frac{1}{{R}_{\,\mathrm{\,net\,}}}=\left({K}_{\,\mathrm{\,Al\,}}+{K}_{\,\mathrm{\,Cu\,}}+{K}_{\,\mathrm{\,Al\,}}\right)\frac{\mathit{A}}{\mathit{l}}``
`` \frac{1}{{R}_{\,\mathrm{\,net\,}}}=\left(200+400+200\right)\times \frac{1}{200}``
`` \Rightarrow {R}_{\,\mathrm{\,net\,}}=\frac{200}{800}``
`` =\frac{1}{4}``
`` ``
`` \,\mathrm{\,Rate\,}\,\mathrm{\,of\,}\,\mathrm{\,heat\,}\,\mathrm{\,flow\,}=\frac{\Delta T}{{R}_{\,\mathrm{\,net\,}}}``
`` =\frac{100}{{\displaystyle \frac{1}{4}}}``
`` =400\,\mathrm{\,W\,}``
Page No 100: