NEET-XII-Physics
28: Heat Transfer
- #31Four identical rods AB, CD, CF and DE are joined as shown in figure (28-E8). The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1, T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.
Figure Ans :
Ans :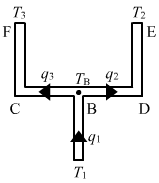
Let the temperature at junction B be T.
Let q1, q2 and q3 be the heat currents, i.e. rate of flow of heat per unit time in AB, BCE and BDF, respectively.
From the diagram, we can see that
q1 = q2 + q3
The rate of flow of heat is givem by
`` q=\frac{KA∆T}{l}``
Using this tn the above equation, we get
`` \frac{KA\left({T}_{1}-T\right)}{l}=\frac{KA\left(T-{T}_{3}\right)}{{\displaystyle \frac{3l}{2}}}+\frac{KA\left(T-{T}_{2}\right)}{{\displaystyle \frac{3l}{2}}}``
`` \Rightarrow {T}_{\mathit{1}}\mathit{-}T\mathit{=}\frac{\mathit{2}\left(\mathit{T}\mathit{-}{\mathit{T}}_{\mathit{3}}\right)}{\mathit{3}}\mathit{+}\frac{\mathit{2}\left(\mathit{T}\mathit{-}{\mathit{T}}_{\mathit{2}}\right)}{\mathit{3}}``
`` \mathit{\Rightarrow }3\left({\mathit{T}}_{\mathit{1}}\mathit{-}\mathit{T}\right)\mathit{=}2T\mathit{-}2{T}_{\mathit{3}}\mathit{+}2T\mathit{-}2{T}_{\mathit{2}}``
`` \mathit{\Rightarrow }T\mathit{=}\frac{\mathit{-}\mathit{3}{\mathit{T}}_{\mathit{1}}\mathit{+}\mathit{2}\left({\mathit{T}}_{\mathit{2}}\mathit{+}{\mathit{T}}_{\mathit{3}}\right)}{\mathit{7}}``
Page No 100: