NEET-XII-Physics
28: Heat Transfer
- #27Suppose the bent part of the frame of the previous problem has a thermal conductivity of 780 J s-1 m-1 °C-1 whereas it is 390 J s-1 m-1°C-1 for the straight part. Calculate the ratio of the rate of heat flow through the bent part to the rate of heat flow through the straight part.Ans :
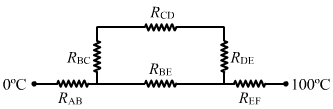
Resistance of any branch, R = `` \frac{l}{KA}``
Here, K is the thermal conductivity, A is the area of cross section and l is the length of the conductor.
`` {R}_{\,\mathrm{\,BC\,}}=\frac{l}{780.\,\mathrm{\,A\,}}=\frac{5\times {10}^{-2}}{780.\,\mathrm{\,A\,}}``
`` {R}_{\,\mathrm{\,CD\,}}=\frac{60\times {10}^{-2}}{780.\,\mathrm{\,A\,}}``
`` {R}_{\,\mathrm{\,DE\,}}=\frac{5\times {10}^{-2}}{780.\,\mathrm{\,A\,}}``
`` {R}_{\,\mathrm{\,AB\,}}=\frac{20\times {10}^{-2}}{390.\,\mathrm{\,A\,}}``
`` {R}_{\,\mathrm{\,EF\,}}=\frac{20\times {10}^{-2}}{390.\,\mathrm{\,A\,}}``
`` {R}_{\,\mathrm{\,BE\,}}=\frac{60\times {10}^{-2}}{390\times \,\mathrm{\,A\,}}``
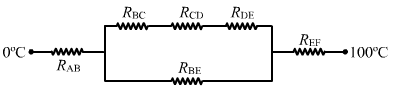
`` {R}_{1}={R}_{\,\mathrm{\,BC\,}}+{R}_{\,\mathrm{\,CD\,}}+{R}_{\,\mathrm{\,DE\,}}=\frac{70\times {10}^{-2}}{780\times \,\mathrm{\,A\,}}``
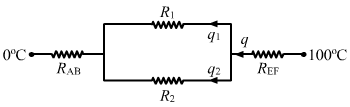
`` {R}_{BE}={R}_{2}=\frac{60\times {10}^{-2}}{390\times A}``
`` ``
`` ``
Since R1 and R2 are in parallel, the amount of heat flowing through them will be same.
`` {q}_{1}{R}_{1}={q}_{2}{R}_{2}``
`` \frac{{q}_{1}}{{q}_{2}}=\frac{{R}_{2}}{{R}_{1}}``
`` =\frac{60\times {10}^{-2}\times 780\times \,\mathrm{\,A\,}}{390\times \,\mathrm{\,A\,}\times 70\times {10}^{-2}}``
`` =\frac{12}{7}``
`` \Rightarrow \frac{{q}_{1}}{{q}_{2}}=\frac{12}{7}``
Page No 100: