NEET-XII-Physics
28: Heat Transfer
- #26Consider the situation shown in figure (28-E5). The frame is made of the same material and has a uniform cross-sectional area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at 100°C is 130 J.
Figure Ans :
Ans :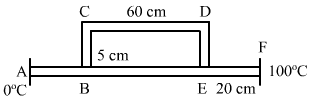
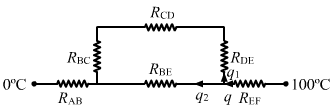
`` {R}_{\,\mathrm{\,BC\,}}=\frac{l}{KA}=\frac{5}{KA}``
`` {R}_{\,\mathrm{\,CD\,}}=\frac{l}{KA}=\frac{60}{KA}``
`` {R}_{\,\mathrm{\,DE\,}}=\frac{5}{KA},{R}_{\,\mathrm{\,AB\,}}=\frac{20}{KA},{R}_{\,\mathrm{\,EF\,}}=\frac{20}{KA}``
`` \,\mathrm{\,Suppose\,}:``
`` {R}_{1}={R}_{\,\mathrm{\,BC\,}}+{R}_{\,\mathrm{\,CD\,}}+{R}_{\,\mathrm{\,DE\,}}=\frac{70}{KA}``
`` \,\mathrm{\,Suppose\,}:``
`` {R}_{\,\mathrm{\,BE\,}}=\frac{60}{KA}={R}_{2}``
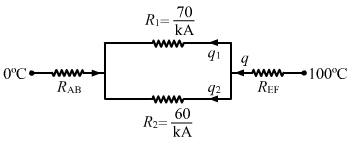
q = q1 + q2 ...(1)
R1 and R2 are in parallel, so total heat across R1 and R2 will be same.
⇒ q1R1 = q2R2
`` {q}_{1}\times \frac{70}{KA}={q}_{2}\times \frac{60}{KA}``
`` 7{q}_{1}=6{q}_{2}``
`` \frac{7{q}_{1}}{6}={q}_{2}...\left(2\right)``
`` ``
From equation (1) and (2),
`` q={q}_{1}+\frac{7{q}_{1}}{6}``
`` q=\frac{13{q}_{1}}{6}``
`` q=130\,\mathrm{\,J\,}``
`` 130=\frac{13{q}_{1}}{6}``
`` {q}_{1}=60\,\mathrm{\,J\,}/\,\mathrm{\,sec\,}``
Page No 100: