Qstnid -Iv-21-a-the Flat Ends Are Maintained At Temperature T1 And T2 (T2 &Gt; T1) (B) The Inside Of The Tube Is Maintained At Temperature T1 And The Outside Is Maintained At T2. (B) The Inside Of The Tube Is Maintained At Temperature T1 And The Outside Is Maintained At T2. - 28: Heat Transfer

Home Learn Fast select Course

Show Unit/Chapter Change Unit Change Subject Last Menu

NEET-XII-Physics

28: Heat Transfer

with Solutions - page 4

Qstn# iv-21-a Prvs-Qstn Next-Qstn

#21-a
the flat ends are maintained at temperature T₁ and T₂ (T₂ > T₁) (b) the inside of the tube is maintained at temperature T₁ and the outside is maintained at T₂. (b) the inside of the tube is maintained at temperature T₁ and the outside is maintained at T₂.
Ans : When the flat ends are maintained at temperatures T₁ and T₂ (where T₂ > T₁):
Area of cross section through which heat is flowing, `` \,\mathrm{\,A\,}=\,\mathrm{\,\pi \,}\left({\,\mathrm{\,R\,}}_{2}^{2}-{\,\mathrm{\,R\,}}_{1}^{2}\right)``

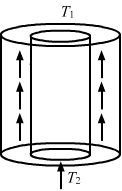
Rate of flow of heat`` =\frac{d\theta }{dt}``
`` =\frac{KA.∆T}{l}``
`` =\frac{K\,\mathrm{\,\pi \,}\left({\,\mathrm{\,R\,}}_{2}^{2}-{\,\mathrm{\,R\,}}_{1}^{2}\right)\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)}{l}`` (b)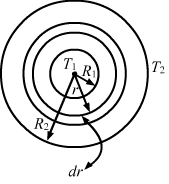
When the inside of the tube is maintained at temperature T₁ and the outside is maintained at T₂_:
Let us consider a cylindrical shell of radius r and thickness dr.
Rate of flow of heat, q`` =KA.\frac{d\,\mathrm{\,T\,}}{dr}``
`` q=KA.\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
`` q=K\left(2\,\mathrm{\,\pi \,}rl\right)\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
`` {\int }_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}\frac{dr}{r}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}{\int }_{{\,\mathrm{\,T\,}}_{1}}^{{\,\mathrm{\,T\,}}_{2}}d\,\mathrm{\,T\,}``
`` {\left[\,\mathrm{\,ln\,}\left(r\right)\right]}_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left[{\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right]``
`` \,\mathrm{\,ln\,}\left(\frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}\right)=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)``
`` q=\frac{2\,\mathrm{\,\pi \,}Kl\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}}\right)}``
Page No 99: (b)
When the inside of the tube is maintained at temperature T₁ and the outside is maintained at T₂_:
Let us consider a cylindrical shell of radius r and thickness dr.
Rate of flow of heat, q`` =KA.\frac{d\,\mathrm{\,T\,}}{dr}``
`` q=KA.\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
`` q=K\left(2\,\mathrm{\,\pi \,}rl\right)\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
`` {\int }_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}\frac{dr}{r}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}{\int }_{{\,\mathrm{\,T\,}}_{1}}^{{\,\mathrm{\,T\,}}_{2}}d\,\mathrm{\,T\,}``
`` {\left[\,\mathrm{\,ln\,}\left(r\right)\right]}_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left[{\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right]``
`` \,\mathrm{\,ln\,}\left(\frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}\right)=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)``
`` q=\frac{2\,\mathrm{\,\pi \,}Kl\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}}\right)}``
Page No 99:

#21-b
the inside of the tube is maintained at temperature T₁ and the outside is maintained at T₂.
Ans :
When the inside of the tube is maintained at temperature T₁ and the outside is maintained at T₂_:
Let us consider a cylindrical shell of radius r and thickness dr.
Rate of flow of heat, q`` =KA.\frac{d\,\mathrm{\,T\,}}{dr}``
`` q=KA.\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
`` q=K\left(2\,\mathrm{\,\pi \,}rl\right)\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
`` {\int }_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}\frac{dr}{r}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}{\int }_{{\,\mathrm{\,T\,}}_{1}}^{{\,\mathrm{\,T\,}}_{2}}d\,\mathrm{\,T\,}``
`` {\left[\,\mathrm{\,ln\,}\left(r\right)\right]}_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left[{\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right]``
`` \,\mathrm{\,ln\,}\left(\frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}\right)=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)``
`` q=\frac{2\,\mathrm{\,\pi \,}Kl\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}}\right)}``
Page No 99: