NEET-XII-Physics
28: Heat Transfer
- #10The left end of a copper rod (length = 20 cm, area of cross section = 0.20 cm2) is maintained at 20°C and the right end is maintained at 80°C. Neglecting any loss of heat through radiation, find
a) the temperature at a point 11 cm from the left end and
(b) the heat current through the rod. Thermal conductivity of copper = 385 W m-1°C-1.Ans :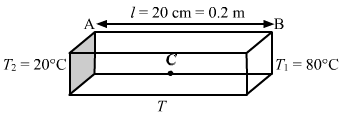
Area of cross section, A = 0.2 cm2 = 0.2 × 10-4 m2
Thermal conductivity, k = 385 W m-1 °C-1
`` \,\mathrm{\,Rate\,}\,\mathrm{\,of\,}\,\mathrm{\,flow\,}\,\mathrm{\,of\,}\,\mathrm{\,heat\,}=\frac{\,\mathrm{\,Temperature\,}\,\mathrm{\,difference\,}}{\,\mathrm{\,Thermal\,}\,\mathrm{\,resistance\,}}``
`` \frac{\,\mathrm{\,\Delta Q\,}}{\,\mathrm{\,\Delta \,}t}=\frac{kA\mathit{(}{T}_{1}-{T}_{2}\mathit{)}}{{\displaystyle l}}``
`` \frac{\,\mathrm{\,\Delta Q\,}}{\,\mathrm{\,\Delta \,}t}=\left(\frac{80-20}{0.2}\right)\times 385\times 0.2\times {10}^{-4}``
`` =2310\times {10}^{-3}``
`` =2.31\,\mathrm{\,J\,}/\,\mathrm{\,sec\,}``
Let te temperature of point C be T, which is at a distance of 11 cm from the left end.
Rate of flow of heat is given by
`` \frac{\,\mathrm{\,\Delta Q\,}}{\,\mathrm{\,\Delta \,}t}=\frac{\,\mathrm{\,k\,}A\,\mathrm{\,\Delta \,}T}{{\displaystyle l}}``
`` \Rightarrow \frac{\,\mathrm{\,\Delta \,}T}{l}=\left(\frac{\,\mathrm{\,\Delta Q\,}}{\,\mathrm{\,\Delta \,}t}\right)\times \frac{1}{\,\mathrm{\,kA\,}}``
`` \frac{T-20}{11\times {10}^{-2}}=\frac{2.31}{383\times 0.2\times {10}^{-4}}``
`` \Rightarrow T=33+20``
`` \Rightarrow T=53°\,\mathrm{\,C\,}``
Page No 99: