NEET-XII-Physics
28: Heat Transfer
- #9Water at 50°C is filled in a closed cylindrical vessel of height 10 cm and cross sectional area 10 cm2. The walls of the vessel are adiabatic but the flat parts are made of 1-mm thick aluminium (K = 200 J s-1 m-1°C-1). Assume that the outside temperature is 20°C. The density of water is 100 kg m-3, and the specific heat capacity of water = 4200 J k-1 g °C-1. Estimate the time taken for the temperature of fall by 1.0 °C. Make any simplifying assumptions you need but specify them.Ans : Area of cross section, A = 10 cm2 = 10 × 10-4 m2
Thermal conductivity, K = 200 Js-1 m-1 °C-1
Height, H = 10 cm
Length, l = 1 mm =10-3 m
Temperature inside the cylindrical vessel, T1 = 50°C
Temperature outside the vessel, T2 = 30°C
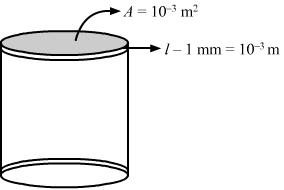
Rate of flow of heat from 1 flat surface will be given by
`` \frac{\Delta Q}{\,\mathrm{\,\Delta \,}t}=\frac{{T}_{1}-{T}_{2}}{{\displaystyle \frac{l}{\,\mathrm{\,kA\,}}}}``
`` \frac{\Delta Q}{\,\mathrm{\,\Delta \,}t}=\frac{\left(50-30\right)\times 200\times {10}^{-3}}{{10}^{-3}}``
`` \frac{\Delta Q}{\,\mathrm{\,\Delta \,}t}=6000\,\mathrm{\,J\,}/\,\mathrm{\,sec\,}``
Heat escapes out from both the flat surfaces.
Net rate of heat flow = 2 × 6000 = 12000 J/sec
`` \frac{\Delta Q}{\,\mathrm{\,\Delta \,}t}=\frac{m·\,\mathrm{\,s\,}·\Delta T}{{\displaystyle \,\mathrm{\,\Delta \,}t}}``
`` ``
Mass = Volume density
⇒ `` {10}^{-3}\times 0.1\times 1000``
`` =0.1\,\mathrm{\,g\,}``
Using this in the above formula for finding the rate of flow of heat, we get
`` 12000=0.1\times 4200\times \left(\frac{\Delta T}{t}\right)``
`` \Rightarrow \frac{\,\mathrm{\,\Delta \,}T}{\,\mathrm{\,\Delta \,}t}=\frac{12000}{420}=28.57``
`` \,\mathrm{\,As\,}\,\mathrm{\,\Delta \,}T=1°\,\mathrm{\,C\,}``
`` \Rightarrow \frac{1}{t}=28.57``
`` \Rightarrow t=\frac{1}{28.57}=0.035\,\mathrm{\,sec\,}``
Page No 98: