HomeLearn Fast select Course
Show Unit/ChapterChange UnitChange SubjectLast Menu
NEET-XII-Physics

26: Laws of Thermodynamics

with Solutions - page 5
Qstn# iv-22 Prvs-Qstn
  • #22
    An adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U = 1.5 nRT) and the part on the right contains two moles of the same gas. Initially, the pressure on each side is p. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and
    (d) the increase in the internal energy of the gas in the left part.
    Ans : (a) Since the conducting wall is fixed, the work done by the gas on the left part during the process is zero because the change in volume will be zero due to the fixed position of the wall. (b) For left side:
    Let the initial pressure on both sides of the wall be p.
    We know,
    Volume =`` \frac{\mathit{V}}{\mathit{2}}``
    Number of moles, n = 1
    Let initial temperature be T1.
    Using the ideal gas equation, we get
    `` \frac{\mathit{P}\mathit{V}}{\mathit{2}}\mathit{=}nR{T}_{\mathit{1}}``
    `` \mathit{\Rightarrow }\frac{\mathit{P}\mathit{V}}{\mathit{2}}\mathit{=}\mathit{\left(}\mathit{1}\mathit{\right)}RT``
    `` \mathit{\Rightarrow }{T}_{\mathit{1}}\mathit{=}\frac{\mathit{P}\mathit{V}}{\mathit{(}\mathit{2}\mathit{m}\mathit{o}\mathit{l}\mathit{e}\mathit{s}\mathit{)}\mathit{R}}``
    For right side:
    Number of moles, n = 2
    Let the initial temperature be T2.
    We know,
    Volume =`` \frac{\mathit{V}}{\mathit{2}}``
    `` \frac{\mathit{P}\mathit{V}}{\mathit{2}}\mathit{=}nR{T}_{\mathit{2}}``
    `` \mathit{\Rightarrow }{T}_{\mathit{2}}\mathit{=}\frac{\mathit{P}\mathit{V}}{\mathit{(}\mathit{4}\mathit{m}\mathit{o}\mathit{l}\mathit{e}\mathit{s}\mathit{)}\mathit{R}}`` (c)

    Here,

    U = 1.5nRT

    T = temperature at the equilibrium

    P1 = P2 = P

    n1 = 1 mol

    n2 = 2 mol

    Let T1 and T2 be the initial temperatures of the left and right chamber respectively.

    Applying eqn. of state


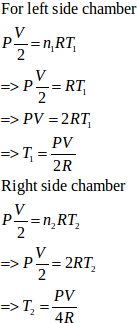
    We know that total n = n1 + n2 = 3
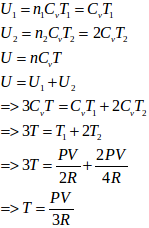    (d) For RHS:
    ∆Q = ∆U as ∆W = 0
    ∆U = 1.5 n2R (T - T2)
    When T is the final temperature and T2 is the initial temperature of side 1, we get
    = 1.5 × 2 × R (T - T2)
    = 1.5 × 2 × `` \frac{4\,\mathrm{\,PV\,}-3\,\mathrm{\,PV\,}}{4\times 3\,\mathrm{\,mole\,}}``
    `` ``
    `` =\frac{3\times \,\mathrm{\,PV\,}}{4\times 3\,\mathrm{\,mole\,}}=\frac{\,\mathrm{\,PV\,}}{4}``
    (d) If dW = 0, then using the first law, we get
    dQ = - dU
    ⇒ dU = - dQ = `` \frac{-\,\mathrm{\,PV\,}}{4}``

  • #22-a
    the work done by the gas in the left part during the process,
    Ans : Since the conducting wall is fixed, the work done by the gas on the left part during the process is zero because the change in volume will be zero due to the fixed position of the wall.
  • #22-b
    the temperature on the two sides in the beginning,
    Ans : For left side:
    Let the initial pressure on both sides of the wall be p.
    We know,
    Volume =`` \frac{\mathit{V}}{\mathit{2}}``
    Number of moles, n = 1
    Let initial temperature be T1.
    Using the ideal gas equation, we get
    `` \frac{\mathit{P}\mathit{V}}{\mathit{2}}\mathit{=}nR{T}_{\mathit{1}}``
    `` \mathit{\Rightarrow }\frac{\mathit{P}\mathit{V}}{\mathit{2}}\mathit{=}\mathit{\left(}\mathit{1}\mathit{\right)}RT``
    `` \mathit{\Rightarrow }{T}_{\mathit{1}}\mathit{=}\frac{\mathit{P}\mathit{V}}{\mathit{(}\mathit{2}\mathit{m}\mathit{o}\mathit{l}\mathit{e}\mathit{s}\mathit{)}\mathit{R}}``
    For right side:
    Number of moles, n = 2
    Let the initial temperature be T2.
    We know,
    Volume =`` \frac{\mathit{V}}{\mathit{2}}``
    `` \frac{\mathit{P}\mathit{V}}{\mathit{2}}\mathit{=}nR{T}_{\mathit{2}}``
    `` \mathit{\Rightarrow }{T}_{\mathit{2}}\mathit{=}\frac{\mathit{P}\mathit{V}}{\mathit{(}\mathit{4}\mathit{m}\mathit{o}\mathit{l}\mathit{e}\mathit{s}\mathit{)}\mathit{R}}``
  • #22-c
    the final common temperature reached by the gases,
    Ans :

    Here,

    U = 1.5nRT

    T = temperature at the equilibrium

    P1 = P2 = P

    n1 = 1 mol

    n2 = 2 mol

    Let T1 and T2 be the initial temperatures of the left and right chamber respectively.

    Applying eqn. of state


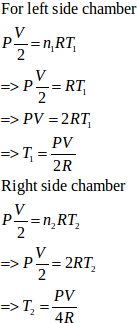
    We know that total n = n1 + n2 = 3

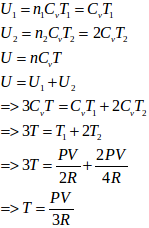
  • #22-d
    the heat given to the gas in the right part and
    (d) the increase in the internal energy of the gas in the left part.
    Ans : For RHS:
    ∆Q = ∆U as ∆W = 0
    ∆U = 1.5 n2R (T - T2)
    When T is the final temperature and T2 is the initial temperature of side 1, we get
    = 1.5 × 2 × R (T - T2)
    = 1.5 × 2 × `` \frac{4\,\mathrm{\,PV\,}-3\,\mathrm{\,PV\,}}{4\times 3\,\mathrm{\,mole\,}}``
    `` ``
    `` =\frac{3\times \,\mathrm{\,PV\,}}{4\times 3\,\mathrm{\,mole\,}}=\frac{\,\mathrm{\,PV\,}}{4}``
    (d) If dW = 0, then using the first law, we get
    dQ = - dU
    ⇒ dU = - dQ = `` \frac{-\,\mathrm{\,PV\,}}{4}``