HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
NEET-XII-Physics

26: Laws of Thermodynamics

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • Qstn #3
    A system can be taken from the initial state p1, V1 to the final state p2, V2 by two different methods. Let â–µQ and â–µW represent the heat given to the system and the work done by the system. Which of the following must be the same in both the methods?
    (a) â–µQ
    (b) â–µW
    (c) â–µQ + â–µW
    (d) â–µQ - â–µW.
    digAnsr:   d
    Ans : (d) ∆Q - ∆W
    ​A system is taken from an initial state to the final state by two different methods. So, work done and heat supplied in both the cases will be different as they depend on the path followed. On the other hand, internal energy of the system (U) is a state function, i.e. it only depends on the final and initial state of the process. They are the same in the above two methods.
    Using the first law of thermodynamics, we get
    `` \Delta Q=\Delta U+\Delta W``
    `` \Rightarrow \Delta U=\Delta Q-\Delta W``
    Here, `` \Delta ``U is the change in internal energy, `` \Delta ``Q is the heat given to the system and `` \Delta ``W is the work done by the system.
    Page No 62:
  • Qstn #4
    Refer to figure. Let â–µU1 and â–µU2 be the change in internal energy in processes A and B respectively, â–µQ be the net heat given to the system in process A + B and â–µW be the net work done by the system in the process A + B.
    Figure
    (a) â–µU1 + â–µU2 = 0.
    (b) â–µU1 - â–µU2 = 0.
    (c) â–µQ - â–µW = 0.
    (d) â–µQ + â–µW = 0
    digAnsr:   a,c
    Ans :
    (a) ​∆U1 + ∆U2 = 0
    (c) ∆    Q - ∆W = 0
    The process that takes place through A and returns back to the same state through B is cyclic. Being a state function, net change in internal energy,     ∆U will be zero, i.e.
    ∆U1 (Change in internal energy in process A) = ∆​U2 (Change in internal energy in process B)
    `` \Rightarrow \Delta U=\Delta {U}_{1}+\Delta {U}_{2}=0``
    Here, ∆U is the total change in internal energy in the cyclic process.
    Using the first law of thermodynamics, we get
    `` \Delta Q-\Delta W=\Delta U``
    Here,     ∆Q is the net heat given to the system in process A + B and ∆W is the net work done by the system in the process A + B.
    Thus,
    ∆Q - ∆W = 0
    Page No 62:
  • Qstn #5
    The internal energy of an ideal gas decreases by the same amount as the work done by the system.
    (a) The process must be adiabatic.
    (b) The process must be isothermal.
    (c) The process must be isobaric.
    (d) The temperature must decrease.
    digAnsr:   a,d
    Ans :
    (a) The process must be adiabatic
    (d) The temperature must decrease.
    Using the first law of thermodynamics, we get
    `` \Delta Q=\Delta W+\Delta U``
    `` \Rightarrow \Delta Q=0\left[\because \Delta W=-\Delta U\right]``
    Thus, no heat is exchanged in the process, i.e. the process is adiabatic and since the internal energy is decreasing, the temperature must decrease because the gas is an ideal gas.
    On the other hand, volume and pressure of the gas are varying, leading to positive work done. So, the process cannot be isochoric and isobaric.
    Page No 62:
  • #
    Section : iv
  • Qstn #1
    A thermally insulated, closed copper vessel contains water at 15°C. When the vessel is shaken vigorously for 15 minutes, the temperature rises to 17°C. The mass of the vessel is 100 g and that of the water is 200 g. The specific heat capacities of copper and water are 420 J kg-1 K-1 and 4200 J kg-1 K-1 respectively. Neglect any thermal expansion.
    Ans : Given:
    The system comprises of an insulated copper vessel that contains water.
    t1 = 15°C, t2 = 17°C
    t1 is the initial temperature of the system
    t2 is the final temperature of the system
    ∆t = Change in the temperature of the system = t2 - t1
    = 17°C - 15°C = 2°C = 275 K
    Mass of the vessel, mv = 100 g = 0.1 kg
    Mass of water, mw = 200 g = 0.2 kg
    Specific heat capacity of copper, cu = 420 J/kg-K
    Specific heat capacity of water, cw = 4200 J/kg-K
  • #1-a
    How much heat is transferred to the liquid-vessel system?
    Ans : Since the system is insulated from the surroundings, no heat is transferred between the system and the surroundings. This implies that the heat transferred to the liquid vessel system is zero. The internal heat is shared between the vessel and water.
  • #1-b
    How much work has been done on this system?
    Ans : Work done on the system`` ={m}_{w}{c}_{w}∆t+{m}_{v}{c}_{u}∆t``
    ⇒ dW = 100 × 10-3 × 420 × 2 + 200 × 10-3 × 4200 × 2
    ⇒ dW = 84 + 84 × 20 = 84 × 21
    ⇒ dW = 1764 J
  • #1-c
    How much is the increase in internal energy of the system?
    Ans : Using the first law of thermodynamics, we get
    `` dQ=dW+dU``
    `` \,\mathrm{\,Here\,},dW=pdV``
    Work is done by the system. Thus, work done is negative.
    ⇒ dQ = 0 (given)
    dU = - dW
    = `` -``(`` -``1764) = 1764 J
    Page No 62:
  • Qstn #2
    Figure shows a paddle wheel coupled to a mass of 12 kg through fixed frictionless pulleys. The paddle is immersed in a liquid of heat capacity 4200 J K-1 kept in an adiabatic container. Consider a time interval in which the 12 kg block falls slowly through 70 cm.
  • #2-a
    How much heat is given to the liquid?
    Ans : Heat is not given to the liquid; instead, the mechanical work done is converted to heat. Also the container is adiabatic. So, no heat can enter or exit the system. This implies that the heat given to the liquid is zero.
  • #2-b
    How much work is done on the liquid?
    Ans : Since the 12 kg mass falls through a distance of 70 cm under gravity, energy is lost by this mass. As this mass is connected to the paddle wheel, energy lost by this mass is gained by the paddle wheel.
    `` \Rightarrow ``Work done on the liquid = PE lost by the 12 kg mass
    Now,
    PE lost by the 12 kg mass = mgh
    = 12 × 10 × 0.70
    = 84 J
  • #2-c
    Calculate the rise in the temperature of the liquid neglecting the heat capacity of the container and the paddle.
    Figure
    Ans : Suppose ∆t is the rise in temperature of the paddle wheel when the system gains energy.
    `` \Rightarrow `` 84 = ms∆t
    If s is the specific heat of the system, then
    84 = 1 × 4200 × ∆t (for 'm' = 1 kg)
    ⇒ `` ∆t=\frac{84}{4200}=\frac{1}{50}=0.02\,\mathrm{\,K\,}``
    Page No 62:
  • Qstn #3
    A 100 kg lock is started with a speed of 2.0 m s-1 on a long, rough belt kept fixed in a horizontal position. The coefficient of kinetic friction between the block and the belt is 0.20.
    Ans : Here,
    m = 100 kg
    u = 2.0 m/s
    v = 0
    μk = 0.2
    a) Internal energy of the belt-block system will decrease when the block will lose its KE in heat due to friction. Thus,
    KE lost =

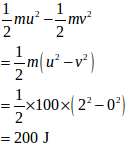
    b) Velocity of the frame is given by
    uf = 2.0 m/s
    u’ = u - uf = 2 - 2= 0
    v’ = 0 - 2 = -2 m/s
    KE lost =

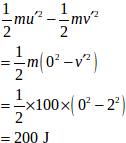
    c) Force of friction is given by

    Page No 62:
  • Qstn #4
    Calculate the change in internal energy of a gas kept in a rigid container when 100 J of heat is supplied to it.
    Ans : Given: Heat supplied to the system, `` ∆``Q = 100 J
    Using the first law of thermodynamics, we get
    `` ∆U=∆Q-∆W``
    Since the container is rigid, initial volume of the system is equal to the final volume of the system. Thus,
    `` ∆``V = `` {V}_{f}-{V}_{i}``= 0
    `` ∆``W = P`` ∆``V = 0
    ∆U = ∆Q = 100 J
    We see that heat supplied to the system is used up in raising the internal energy of the system.
    Page No 62:
  • Qstn #5
    The pressure of a gas changes linearly with volume from 10 kPa, 200 cc to 50 kPa, 50 cc.
    Ans : Initial pressure of the system, P1 = 10 kPa = 10 × 103 Pa
    Final pressure of the system, P2 = 50 kPa = 50 × 103 Pa
    Initial volume of the system, V1 = 200 cc
    Final volume of the system, V2 = 50 cc
next page