NEET-XII-Physics
neet 2020 questions with solutions year:2020
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #30In Young’s double slit experiment, if the separation between coherent sources is halved and the distance of the screen from the coherent sources is doubled, then the fringe width becomes:
(A)double
(B)half
(C)four times
(D)one-fourth
digAnsr: CAns : Fringe width, `` \beta=\frac{\lambda\,D}{d} ``
`` \beta' = \frac{\lambda\,D'}{d'} ``
Now, `` d'=\frac{d}{2} `` and
`` D'=2\,D ``
So, `` \beta'=\frac{\lambda \times 2 D}{d / 2} ``
`` =\frac{4 \,\lambda\,D}{d} ``
`` \beta'=4\,\beta ``
Fringe width becomes 4 times
- Qstn #31The capacitance of a parallel plate capacitor with air as medium is `` 6\, \mu F `` . With the introduction of a dielectric medium, the capacitance becomes 30 `` \mu F. `` The permittivity of the medium is :
`` (\epsilon_0 = 8.85 \times 10^{-12} C^2N^{-1}m^{-2} `` )
(A) `` 0.44 \times 10^{-13} C^2 N^{-1}m^{-2} ``
(B) `` 1.77 \times 10^{-12} C^2 N^{-1}m^{-2} ``
(C) `` 0.44 \times 10^{-10} C^2 N^{-1}m^{-2} ``
(D) `` 5.00 \,C^2 N^{-1}m^{-2} ``
digAnsr: AAns : `` C=KC_{0} ``
`` K=\frac{C}{C_{0}} ``
`` =\frac{30}{6}=5 ``
`` K=\frac{\varepsilon}{\varepsilon_{0}} ``
`` \varepsilon=K\,\varepsilon_{0} ``
`` =5 \times 8.85\times 10^{-12} ``
`` =0.44 \times 10^{-10}\,C^{2}\,N^{-1}\,m^{-2} ``
- Qstn #32Dimensions of stress are:
(A) `` [MLT^{-2}] ``
(B) `` [ML^2T^{-2}] ``
(C) `` [M^1L^{-1}T^{-2}] ``
(D) `` [ML^{-2} T^{-2}] ``digAnsr: C:
- Qstn #33Assume that light of wavelength `` 600\, nm `` is coming from a star. The limit of resolution of telescope whose objective has a diameter of `` 2\,m `` is :
(A) `` 3.66 \times 10^{-7} \,rad ``
(B) `` 1.83 \times 10^{-7} \,rad ``
(C) `` 7.32 \times 10^{-7} \,rad ``
(D) `` 6.00 \times 10^{-7} \,rad ``
digAnsr: AAns : Limit of resolution,
`` \theta_{R}=1.22 \frac{\lambda}{d} `` ;
`` \lambda=600 \times 10^{-9}\,m ``
`` d=2\,m ``
`` \theta_{R}=\frac{1.22 \times 600 \times 10^{-9}}{2} ``
`` \theta_{R}=3.66 \times 10^{-7} `` rad
- Qstn #34A series LCR circuit is connected to an ac voltage source. When L is removed from the circuit, the phase difference between current and voltage is `` \frac {\pi}{3} `` . If instead C is removed from the circuit, the phase difference is again `` \frac {\pi}{3} `` between current and voltage. The power factor of the circuit is :
(A)zero
(B)0.5
(C)1.0
(D)-1.0
digAnsr: CAns : When L is removed,
`` tan\,\phi=\frac{\left|X_{C}\right|}{R} ``
`` \Rightarrow tan \frac{\pi}{3}=\frac{X_{c}}{R} \ldots\left(i\right) ``
When C is removed,
`` tan \,\phi=\frac{\left|X_{L}\right|}{R} ``
`` \Rightarrow tan \frac{\pi}{3}=\frac{X_{L}}{R} \ldots\left(ii\right) ``
From `` \left(i\right) `` and `` \left(ii\right) `` ,
Since `` X_{L}=X_{C} `` , the circuit is in resonance
`` Z=R ``
Power factor `` =cos\,\phi=\frac{R}{Z}=1 ``
- Qstn #35A short electric dipole has a dipole moment of `` 16 \times 10^{-9} C\, m `` . The electric potential due to the dipole at a point at a distance of `` 0.6 \,m `` from the centre of the dipole, situated on a line making an angle of 60° with the dipole axis is :
`` (\frac {1}{4\pi \epsilon_o}= 9 \times 10^9 N\,m^2/C^2) ``
(A) `` 50\,V ``
(B) `` 200\,V ``
(C) `` 400\,V ``
(D)zero
digAnsr: BAns : The electric potential due to the dipole,
`` V=\frac{kp\,cos\,theta}{r^{2}} ``
`` =\frac{9\times 10^{9}\times 16\times 10^{-9}}{(0.6)^{2}}\times \frac{1}{2} ``
`` V=200\,V ``
- Qstn #36An iron rod of susceptibility 599 is subjected to a magnetising field of 1200 A `` m^{-1} `` . The permeability of the material of the rod is :
`` (\mu_o = 4\pi \times 10^{-7} T\,m\,A^{-1}) ``
(A) `` 2.4 \pi \times 10^{-4} T\,m\,A^{-1} ``
(B) `` 8.0 \pi \times 10^{-5} T\,m\,A^{-1} ``
(C) `` 2.4 \pi \times 10^{-5} T\,m\,A^{-1} ``
(D) `` 2.4 \pi \times 10^{-7} T\,m\,A^{-1} ``
digAnsr: AAns : Given, `` \chi_{m}=599 ``
Also, `` \mu_{r}=1+\chi_{m}=600 ``
We know, `` \mu=\mu_{r}\mu_{o} ``
`` \mu=600\times4\pi\times10^{-7} ``
`` \mu=2400\pi\times10^{-7} ``
`` \mu=2.4\pi\times10^{-4}\,T\,m\,A^{-1} ``
- Qstn #37A long solenoid of `` 50\,cm `` length having `` 100\,turns `` carries a current of `` 2.5\,A `` . The magnetic field at the centre of the solenoid is :
`` (\mu_o = 4\pi \times 10^{-7} T\,m\,A^{-1}) ``
(A) `` 6.28 \times 10^{-4}T ``
(B) `` 3.14 \times 10^{-4}T ``
(C) `` 6.28 \times 10^{-5}T ``
(D) `` 3.14 \times 10^{-5}T ``
digAnsr: AAns : Magnetic field at centre of solenoid `` =\mu_{0}nI ``
`` n=\frac{N}{L} ``
`` =\frac{100}{50 \times 10^{-2}} ``
`` =200 `` tums/m
`` I = 2.5 \,A ``
On putting the values,
`` B=4\pi\times 10^{-7}\times 200 \times 2.5 ``
`` =6.28 \times 10^{-4}\,T ``
- Qstn #38A charged particle having drift velocity of `` 7.5 \times 10^{-4} \,m\,s^{-1} `` in an electric field of `` 3 \times 10^{-10}Vm^{-1} `` , has a mobility in `` m^2V^{-1}s^{-1} `` of:
(A) `` 2.25 \times 10^{15} ``
(B) `` 2.5 \times 10^{6} ``
(C) `` 2.5 \times 10^{-6} ``
(D) `` 2.25 \times 10^{-15} ``
digAnsr: BAns : Mobility, `` \mu =\frac{v_{d}}{E} ``
`` =\frac{7.5 \times 10^{-4}}{3 \times 10^{-10}} ``
`` =2.5 \times 10^{6} ``
- Qstn #39The quantities of heat required to raise the temperature of two solid copper spheres of radii `` r_1 `` and `` r_2 `` `` (r_1 = 1.5 \,r_2 `` ) through 1 K are in the ratio :
(A) `` \frac {27}{8} ``
(B) `` \frac {9}{4} ``
(C) `` \frac {3}{2} ``
(D) `` \frac {5}{3} ``
digAnsr: AAns : Heat supplied `` \Delta\,Q =MS\,\Delta\,T ``
For same material ‘s’ remains the same
`` \Delta\,Q \propto\,M `` and `` M=\frac{4}{3}\pi\,r^{3}\,\rho ``
`` \Rightarrow \frac{\Delta\,Q_{1}}{\Delta\,Q_{2}} ``
`` =\left(\frac{r_{1}}{r_{2}}\right)^{3} ``
`` =\left(\frac{1.5}{1}\right)^{3} ``
`` =\frac{27}{8} ``
- Qstn #40An electron is accelerated from rest through a potential difference of V volt. If the de Broglie wavelength of the electron is `` 1.227 \times 10^{-2}nm `` , the potential difference is :
(A) `` 10 `` V
(B) `` 10^2 `` V
(C) `` 10^3 `` V
(D) `` 10^4 `` V
digAnsr: DAns : `` \lambda = 1.227 \times 10^{-2}\,m ``
`` =0.1227 \, Å ``
`` \lambda=\frac{12.27}{\sqrt{V}} Å ``
`` 0.1227 = \frac{12.27}{\sqrt{V}} Å ``
`` \sqrt{V}\times10^{2} ``
`` \Rightarrow V=10^{4} ``
- Qstn #41Taking into account of the significant figures, what is the value of `` 9.99 \,m - 0.0099 \,m `` ?
(A)9.9801 m
(B)9.98 m
(C)9.980 m
(D)9.9 m
digAnsr: BAns : In subtraction the number of decimal places in the result should be equal to the number of decimal places of that term in the operation which contain lesser number of decimal places
`` 9.99 ``
`` \frac{-0.0099}{9.9801} ``
`` \to 9.98\,m `` upto 3 significant figures
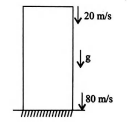
- Qstn #42A ball is thrown vertically downward with a velocity of 20m/s from the top of a tower. It hits the ground after some time with a velocity of 80m/s. The height of the tower is : (g = `` 10m/s^2 `` )
(A)360 m
(B)340 m
(C)320 m
(D)300 m
digAnsr: DAns : Using, `` v^{2}=u^{2}+2gh ``
Given, `` V=80m/s `` and `` u=20 m/s ``
`` h=\frac{v^{2}-u^{2}}{2g} ``
`` =\frac{6400-400}{20} ``
`` =300\,m ``
- Qstn #43A capillary tube of radius `` r `` is immersed in water and water rises in it to a height h. The mass of the water in the capillary is `` 5\,g `` . Another capillary tube of radius `` 2\,r `` is immersed in water. Themass of water that will rise in this tube is :
(A)2.5 g
(B)5.0 g
(C)10.0 g
(D)20.0 gdigAnsr: C:
- Qstn #44A resistance wire connected in the left gap of a metre bridge balances a `` 10\, \Omega `` resistance in the right gap at a point which divides the bridge wire in the ratio `` 3 : 2 `` . If the length of the resistance wire is `` 1.5\,m `` , then the length of 1 `` \Omega `` of the resistance wire is:
(A) `` 1.0 \times 10^{-2} m ``
(B) `` 1.0 \times 10^{-1} m ``
(C) `` 1.5 \times 10^{-1} m ``
(D) `` 1.5 \times 10^{-2} m ``
digAnsr: BAns :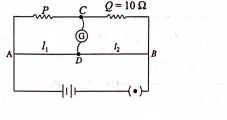
Initially, `` \frac{P}{10}=\frac{l_{1}}{l_{2}}=\frac{3}{2} ``
`` \Rightarrow P=\frac{30}{2}=15\Omega ``
Now resistance, `` R=\frac{\rho\,l}{A} ``
`` \frac{R_{1}}{R_{2}}=\frac{l_{1}}{l_{2}} `` : Length of `` 15\,\Omega `` resistance wire is 1.5 m
`` \Rightarrow \frac{15}{1}=\frac{1.5}{l_{2}} ``
`` \Rightarrow l_{2}=0.1\,m ``
`` =1.0 \times 10^{-1}\,m ``
`` \therefore `` Length of `` 1\,\Omega `` resistance wire is `` 1.0\times 10^{-1}\,m ``