NEET-XII-Physics
09: Ray Optics And Optical Instruments
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #26A myopic person has been using spectacles of power -1.0 dioptre for distant vision. During old age he also needs to use separate reading glass of power + 2.0 dioptres. Explain what may have happened.
Ans : The power of the spectacles used by the myopic person, P = -1.0 D
Focal length of the spectacles,
Hence, the far point of the person is 100 cm. He might have a normal near point of 25 cm. When he uses the spectacles, the objects placed at infinity produce virtual images at 100 cm. He uses the ability of accommodation of the eye-lens to see the objects placed between 100 cm and 25 cm.
During old age, the person uses reading glasses of power,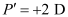
The ability of accommodation is lost in old age. This defect is called presbyopia. As a result, he is unable to see clearly the objects placed at 25 cm.
- Qstn #27A person looking at a person wearing a shirt with a pattern comprising vertical and horizontal lines is able to see the vertical lines more distinctly than the horizontal ones. What is this defect due to? How is such a defect of vision corrected?
Ans : In the given case, the person is able to see vertical lines more distinctly than horizontal lines. This means that the refracting system (cornea and eye-lens) of the eye is not working in the same way in different planes. This defect is called astigmatism. The person’s eye has enough curvature in the vertical plane. However, the curvature in the horizontal plane is insufficient. Hence, sharp images of the vertical lines are formed on the retina, but horizontal lines appear blurred. This defect can be corrected by using cylindrical lenses.
- Qstn #28A man with normal near point (25 cm) reads a book with small print using a magnifying glass: a thin convex lens of focal length 5 cm.
- #28-aWhat is the closest and the farthest distance at which he should keep the lens from the page so that he can read the book when viewing through the magnifying glass?Ans : Focal length of the magnifying glass, f = 5 cm
Least distance of distance vision, d = 25 cm
Closest object distance = u
Image distance, v = -d = -25 cm
According to the lens formula, we have:
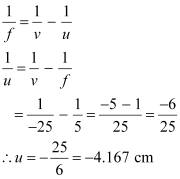
Hence, the closest distance at which the person can read the book is 4.167 cm.
For the object at the farthest distant (u’), the image distance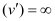
According to the lens formula, we have:
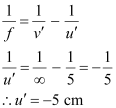
Hence, the farthest distance at which the person can read the book is
5 cm.
- #28-bWhat is the maximum and the minimum angular magnification (magnifying power) possible using the above simple microscope?Ans : Maximum angular magnification is given by the relation:
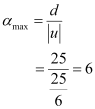
Minimum angular magnification is given by the relation:
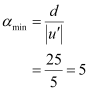
- Qstn #29A card sheet divided into squares each of size 1 mm2 is being viewed at a distance of 9 cm through a magnifying glass (a converging lens of focal length 9 cm) held close to the eye.
-(a) What is the magnification produced by the lens? How much is the area of each square in the virtual image?
(b) What is the angular magnification (magnifying power) of the lens?
(c) Is the magnification in (a) equal to the magnifying power in (b)?
Explain.
Ans : Note : Here we took focal Length as 10 cm because if we takeit as 9 cm then image distance will be zero ,which does not make any sense. (a) Area of each square, A = 1 mm2
Object distance, u = -9 cm
Focal length of a converging lens, f = 9cm
For image distance v, the lens formula can be written as:
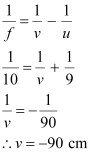
Magnification,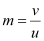
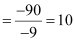
∴Area of each square in the virtual image = (10)2A
= 102 × 1 = 100 mm2
= 1 cm2
(b) Magnifying power of the lens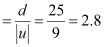
(c) The magnification in (a) is not the same as the magnifying power in (b).
The magnification magnitude is and the magnifying power is
and the magnifying power is .
.
The two quantities will be equal when the image is formed at the near point (25 cm).
- #30
- #30-aAt what distance should the lens be held from the figure in
Exercise 9.29 in order to view the squares distinctly with the maximum possible magnifying power?
Ans : The maximum possible magnification is obtained when the image is formed at the near point (d = 25 cm).
Image distance, v = -d = -25 cm
Focal length, f = 10 cm
Object distance = u
According to the lens formula, we have:

Hence, to view the squares distinctly, the lens should be kept 7.14 cm away from them.
- #30-bWhat is the magnification in this case?Ans : Magnification =
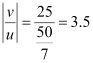
- #30-cIs the magnification equal to the magnifying power in this case?
Explain.
Ans : Magnifying power =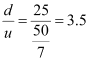
Since the image is formed at the near point (25 cm), the magnifying power is equal to the magnitude of magnification.
- Qstn #31What should be the distance between the object in Exercise 9.30 and the magnifying glass if the virtual image of each square in the figure is to have an area of 6.25 mm2. Would you be able to see the squares distinctly with your eyes very close to the magnifier?
[Note: Exercises 9.29 to 9.31 will help you clearly understand the difference between magnification in absolute size and the angular magnification (or magnifying power) of an instrument.]
Ans : Area of the virtual image of each square, A = 6.25 mm2
Area of each square, A0 = 1 mm2
Hence, the linear magnification of the object can be calculated as:
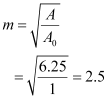
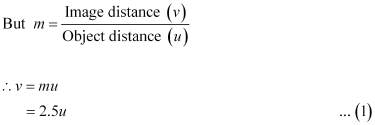
Focal length of the magnifying glass, f = 10 cm
According to the lens formula, we have the relation:

The virtual image is formed at a distance of 15 cm, which is less than the near point (i.e., 25 cm) of a normal eye. Hence, it cannot be seen by the eyes distinctly.
- #32-aThe angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense then does a magnifying glass provide angular magnification?Ans : Though the image size is bigger than the object, the angular size of the image is equal to the angular size of the object. A magnifying glass helps one see the objects placed closer than the least distance of distinct vision (i.e., 25 cm). A closer object causes a larger angular size. A magnifying glass provides angular magnification. Without magnification, the object cannot be placed closer to the eye. With magnification, the object can be placed much closer to the eye.
- #32-bIn viewing through a magnifying glass, one usually positions one’s eyes very close to the lens. Does angular magnification change if the eye is moved back?Ans : Yes, the angular magnification changes. When the distance between the eye and a magnifying glass is increased, the angular magnification decreases a little. This is because the angle subtended at the eye is slightly less than the angle subtended at the lens. Image distance does not have any effect on angular magnification.
- #32-cMagnifying power of a simple microscope is inversely proportional to the focal length of the lens. What then stops us from using a convex lens of smaller and smaller focal length and achieving greater and greater magnifying power?Ans : The focal length of a convex lens cannot be decreased by a greater amount. This is because making lenses having very small focal lengths is not easy. Spherical and chromatic aberrations are produced by a convex lens having a very small focal length.