NEET-XII-Physics
08: Electromagnetic Waves
- #10In a plane electromagnetic wave, the electric field oscillates sinusoidally at a frequency of 2.0 × 1010 Hz and amplitude 48 V m-1.
(a) What is the wavelength of the wave?
(b) What is the amplitude of the oscillating magnetic field?
(c) Show that the average energy density of the E field equals the average energy density of the B field. [c = 3 × 108 m s-1.]
(a) What is the wavelength of the wave?
(b) What is the amplitude of the oscillating magnetic field?
(c) Show that the average energy density of the E field equals the average energy density of the B field. [c = 3 × 108 m s-1.]
(a) What is the wavelength of the wave?
(b) What is the amplitude of the oscillating magnetic field?
(c) Show that the average energy density of the E field equals the average energy density of the B field. [c = 3 × 108 m s-1.]Ans : Frequency of the electromagnetic wave, ν = 2.0 × 1010 Hz
Electric field amplitude, E0 = 48 V m-1
Speed of light, c = 3 × 108 m/s
(a) Wavelength of a wave is given as:
(b) Magnetic field strength is given as:
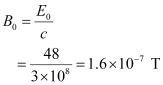
(c) Energy density of the electric field is given as:
And, energy density of the magnetic field is given as:
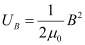
Where,
∈0 = Permittivity of free space
μ0 = Permeability of free space
We have the relation connecting E and B as:
E = cB ... (1)
Where,
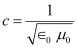... (2)
Putting equation (2) in equation (1), we get
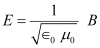
Squaring both sides, we get
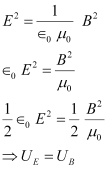
(a) Wavelength of a wave is given as:
(b) Magnetic field strength is given as:
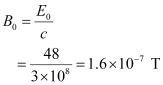
(c) Energy density of the electric field is given as:
And, energy density of the magnetic field is given as:
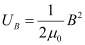
Where,
∈0 = Permittivity of free space
μ0 = Permeability of free space
We have the relation connecting E and B as:
E = cB ... (1)
Where,
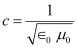... (2)
Putting equation (2) in equation (1), we get
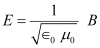
Squaring both sides, we get
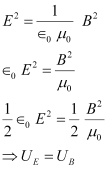
(a) Wavelength of a wave is given as:
(b) Magnetic field strength is given as:
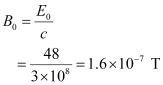
(c) Energy density of the electric field is given as:
And, energy density of the magnetic field is given as:
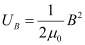
Where,
∈0 = Permittivity of free space
μ0 = Permeability of free space
We have the relation connecting E and B as:
E = cB ... (1)
Where,
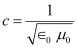... (2)
Putting equation (2) in equation (1), we get
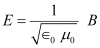
Squaring both sides, we get
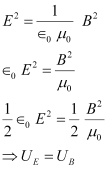
- #10-aWhat is the wavelength of the wave?Ans : Wavelength of a wave is given as:
- #10-bWhat is the amplitude of the oscillating magnetic field?Ans : Magnetic field strength is given as:
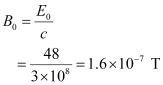
- #10-cShow that the average energy density of the E field equals the average energy density of the B field. [c = 3 × 108 m s-1.]Ans : Energy density of the electric field is given as:
And, energy density of the magnetic field is given as:
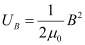
Where,
∈0 = Permittivity of free space
μ0 = Permeability of free space
We have the relation connecting E and B as:
E = cB ... (1)
Where,
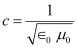... (2)
Putting equation (2) in equation (1), we get
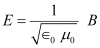
Squaring both sides, we get