NEET-XII-Physics
03: Current Electricity
- #9Determine the current in each branch of the network shown in fig 3.30:
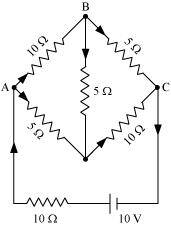
Ans : Current flowing through various branches of the circuit is represented in the given figure.
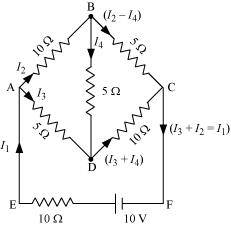
I1 = Current flowing through the outer circuit
I2 = Current flowing through branch AB
I3 = Current flowing through branch AD
I2 - I4 = Current flowing through branch BC
I3 + I4 = Current flowing through branch CD
I4 = Current flowing through branch BD
For the closed circuit ABDA, potential is zero i.e.,
10I2 + 5I4 - 5I3 = 0
2I2 + I4 -I3 = 0
I3 = 2I2 + I4 ... (1)
For the closed circuit BCDB, potential is zero i.e.,
5(I2 - I4) - 10(I3 + I4) - 5I4 = 0
5I2 + 5I4 - 10I3 - 10I4 - 5I4 = 0
5I2 - 10I3 - 20I4 = 0
I2 = 2I3 + 4I4 ... (2)
For the closed circuit ABCFEA, potential is zero i.e.,
-10 + 10 (I1) + 10(I2) + 5(I2 - I4) = 0
10 = 15I2 + 10I1 - 5I4
3I2 + 2I1 - I4 = 2 ... (3)
From equations (1) and (2), we obtain
I3 = 2(2I3 + 4I4) + I4
I3 = 4I3 + 8I4 + I4
- 3I3 = 9I4
- 3I4 = + I3 ... (4)
Putting equation (4) in equation (1), we obtain
I3 = 2I2 + I4
- 4I4 = 2I2
I2 = - 2I4 ... (5)
It is evident from the given figure that,
I1 = I3 + I2 ... (6)
Putting equation (6) in equation (1), we obtain
3I2 +2(I3 + I2) - I4 = 2
5I2 + 2I3 - I4 = 2 ... (7)
Putting equations (4) and (5) in equation (7), we obtain
5(-2 I4) + 2(- 3 I4) - I4 = 2
- 10I4 - 6I4 - I4 = 2
17I4 = - 2
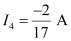
Equation (4) reduces to
I3 = - 3(I4)
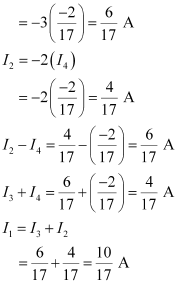
Therefore, current in branch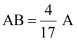
In branch BC =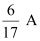
In branch CD =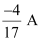
In branch AD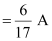
In branch BD =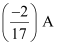
Total current =