NEET-XII-Physics
02: Electrostatic Potential And Capacitance
- #16null (a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
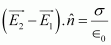
Where
is a unit vector normal to the surface at a point and σ is the surface charge density at that point. (The direction of is from side 1 to side 2.) Hence show that just outside a conductor, the electric field is σ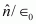 
(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another. [Hint: For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]Ans : null (a) Electric field on one side of a charged body is E1 and electric field on the other side of the same body is E2. If infinite plane charged body has a uniform thickness, then electric field due to one surface of the charged body is given by,
Where,
= Unit vector normal to the surface at a point
σ = Surface charge density at that point
Electric field due to the other surface of the charged body,
Electric field at any point due to the two surfaces,
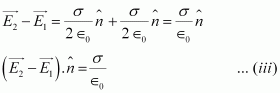
Since inside a closed conductor,
= 0,
∴
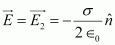
Therefore, the electric field just outside the conductor is
.
(b) When a charged particle is moved from one point to the other on a closed loop, the work done by the electrostatic field is zero. Hence, the tangential component of electrostatic field is continuous from one side of a charged surface to the other.
- #16-aShow that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
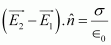
Where
is a unit vector normal to the surface at a point and σ is the surface charge density at that point. (The direction of is from side 1 to side 2.) Hence show that just outside a conductor, the electric field is σ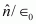
Ans : Electric field on one side of a charged body is E1 and electric field on the other side of the same body is E2. If infinite plane charged body has a uniform thickness, then electric field due to one surface of the charged body is given by,
Where,
= Unit vector normal to the surface at a point
σ = Surface charge density at that point
Electric field due to the other surface of the charged body,
Electric field at any point due to the two surfaces,
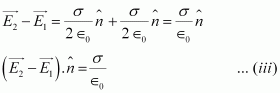
Since inside a closed conductor, = 0,
∴
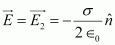
Therefore, the electric field just outside the conductor is.
- #16-bShow that the tangential component of electrostatic field is continuous from one side of a charged surface to another. [Hint: For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]Ans : When a charged particle is moved from one point to the other on a closed loop, the work done by the electrostatic field is zero. Hence, the tangential component of electrostatic field is continuous from one side of a charged surface to the other.