NEET-XI-Physics
14: Oscillations
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #10In Exercise 9, let us take the position of mass when the spring is unstreched as x = 0, and the direction from left to right as the positive direction of x - axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is (a) at the mean position, (b) at the maximum stretched position, and (c) at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?
Ans :
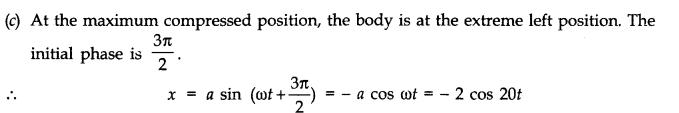
Note: The functions neither differ in amplitude nor in frequency . They differ only in initial phase.
- Qstn #11Following figures correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e., clockwise or anticlockwise) are indicated on each figure.
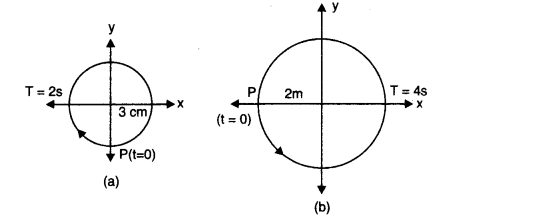
Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P in each case.
Ans :
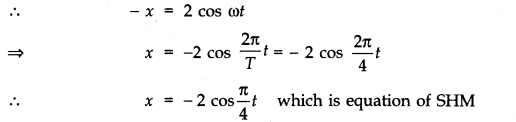
- Qstn #12Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t = 0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anti-clockwise in every case:
(x is in cm and t is in s)
(a) x = - 2 sin (3t + ``\pi`` /3)
(b) x = cos (``\pi`` /6 - t)
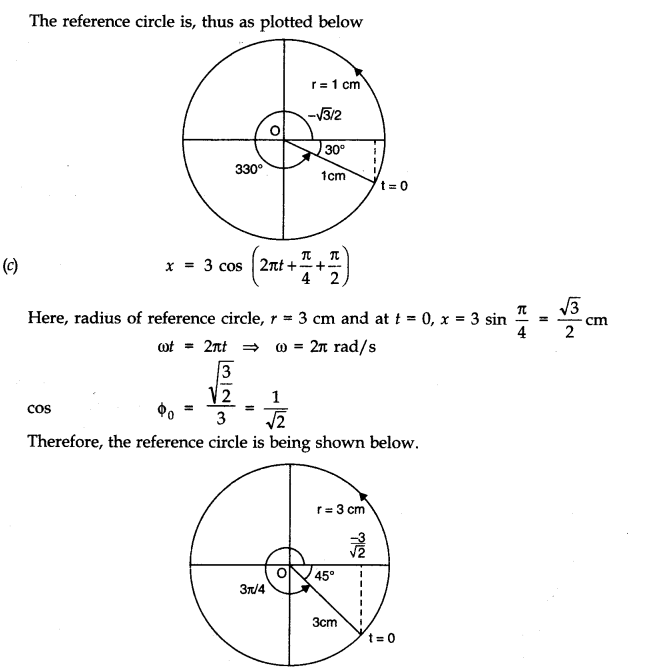
(c) x = 3 sin (2``\pi``t + ``\pi`` /4)
(d) x = 2 cos ``\pi`` t.Ans :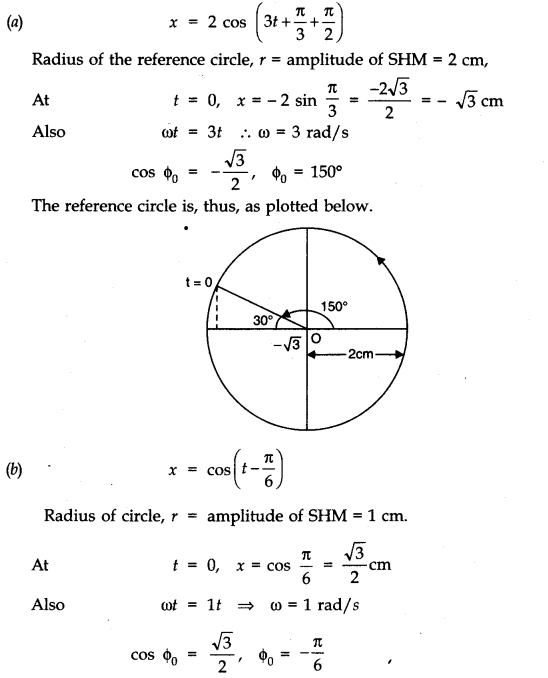

- Qstn #13Figure (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure (b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in Figure - (b) is stretched by the same force F.
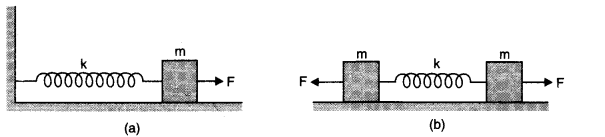
(a) What is the maximum extension of the spring in the two cases?
(b) If the mass in Fig. (a) and the two masses in Fig. (b) are released free, what is the period of oscillation in each case?Ans :
- Qstn #14The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rev/min, what its maximum speed?Ans :


- Qstn #15The acceleration due to gravity on the surface of moon is 1.7 ms-2. What is the time period of a simple pendulum on the surface of moon if its time-period on the surface of Earth is 3.5 s? (g on the surface of Earth is 9.8 ms-2.)Ans :

- #16-aAns :

- #16-bAns :

- #16-cAns : The wrist watch uses an electronic system or spring system to give the time, which does not change with acceleration due to gravity. Therefore, watch gives the correct time.
- #16-dAns : During free fall of the cabin, the acceleration due to gravity is zero. Therefore, the frequency of oscillations is also zero i.e., the pendulum will not vibrate at all.
- Qstn #17A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?Ans : In this case, the bob of the pendulum is under the action of two accelerations.

- Qstn #18A cylindrical piece of cork of density of base area A and height h floats in a liquid of density ``\rho``1 . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
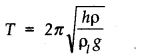
where ``\rho`` is the density of cork. (Ignore damping due to viscosity of the liquid).
Ans :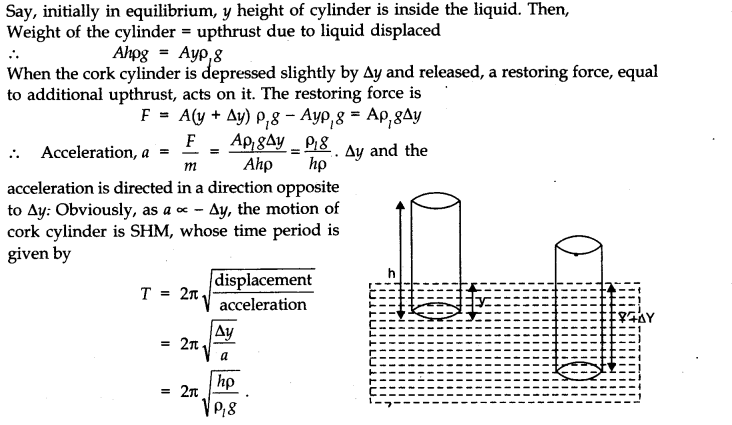
- Qstn #19One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere.
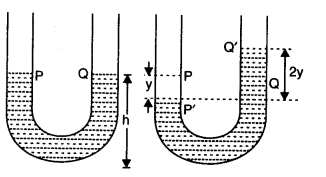
A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
Ans : The suction pump creates the pressure difference, thus mercury rises in one limb of the U-tube. When it is removed, a net force acts on the liquid column due to the difference in levels of mercury in the two limbs and hence the liquid column executes S.H.M. which can be expressed as:
Consider the mercury contained in a vertical U-tube upto the level P and Q in its two limbs.
Let P = density of the mercury.
L = Total length of the mercury column in both the limbs.
A = internal cross-sectional area of U-tube. m = mass of mercury in U-tube = LAP.
Assume, the mercury be depressed in left limb to F by a small distance y, then it rises by the same amount in the right limb to position Q’.
.’. Difference in levels in the two limbs = P’ Q’ = 2y.
:. Volume of mercury contained in the column of length 2y = A X 2y
.•. m - A x 2y x ``\rho``.
If W = weight of liquid contained in the column of length 2y.
Then W = mg = A x 2y x ``\rho`` x g
This weight produces the restoring force (F) which tends to bring back the mercury to its equilibrium position.

- Qstn #20An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.). Shaw that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal.
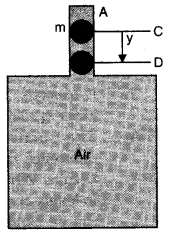
Ans : Consider an air chamber of volume V with a long neck of uniform area of cross-section A, and a frictionless ball of mass m fitted smoothly in the neck at position C, Fig. The pressure of air below the ball inside the chamber is equal to the atmospheric pressure.
Increase the pressure on the ball by a little amount p, so that the ball is depressed to position D, where CD = y.
There will be decrease in volume and hence increase in pressure of air inside the chamber. The decrease in volume of the air inside the chamber, ΔV = Ay


Note. If the ball oscillates in the neck of chamber under isothermal conditions, thru E = P = picture of air inside the chamber, when ball is at equilibrium position. If the ball oscillate in the neck of chamber under adiabatic conditions, then E = gP. where g = Cp/Cv.
