NEET-XI-Physics
14: Oscillations
- #4-0Which of the following function of time represent |a) simple harmonic,(b)periodic but not simple harmonic, and non-periodic motion? Give period for each case of periodic motion (to is any positive constant).nullnullnullnullnullnullnullnullnullnullnullnull
(1) (a) sin wt - cos wt (2) (b) sin3 wt (3) (c) 3 cos -2 cos (``\pi``/4-2 wt) (4) (d) cos wt + cos 3 wt + cos 5 wt
(5) (e) ``e^{-w^2t^2}`` (6) (f) 1 + wt + w2t2. (1) (a) sin wt - cos wt (2) (b) sin3 wt (3) (c) 3 cos -2 cos (``\pi``/4-2 wt) (4) (d) cos wt + cos 3 wt + cos 5 wt
(5) (e) ``e^{-w^2t^2}`` (6) (f) 1 + wt + w2t2.Ans : The function will represent a periodic motion, if it is identically repeated after a fixed interval of time and will represent S.H.M if it can be written uniquely in the form of a cos

(1) ``\sin \omega t - \cos \omega t``
=``\sin\omega t - \sin(\pi/2 -\omega t)`` ( as ``cos (\pi/2-\theta) = \sin \theta``)
(Again (`` \sin A - \sin B = 2\sin \frac{A-B}{2} \cos\frac{A+B}{2}``)
=``2 \cos \pi/4 \sin(\omega t - \pi/4)``
= ``\sqrt{2} \sin(\omega t - \pi/4)``
( shm equation ``x(t) = a\sin(\omega t + \alpha)``
comparing with shm,
A= ``\sqrt2`` and Time period T = ``2\pi/\omega`` and phase angle = ``\pi/4`` or ``( 2\pi-\pi/4) = 7\pi/4``.
(2) (3)
(3) 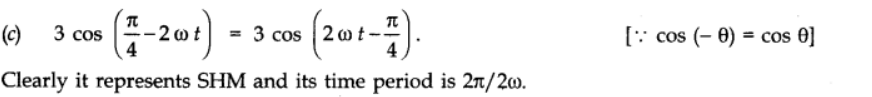
(4) (5) (e) e-w2t2 . It is an exponential function which never repeats itself. Therefore it represents non-periodic motion.
(5) (e) e-w2t2 . It is an exponential function which never repeats itself. Therefore it represents non-periodic motion.
(6) (f) 1 + wt + w2t2 also represents non periodic motion. (1) ``\sin \omega t - \cos \omega t``
=``\sin\omega t - \sin(\pi/2 -\omega t)`` ( as ``cos (\pi/2-\theta) = \sin \theta``)
(Again (`` \sin A - \sin B = 2\sin \frac{A-B}{2} \cos\frac{A+B}{2}``)
=``2 \cos \pi/4 \sin(\omega t - \pi/4)``
= ``\sqrt{2} \sin(\omega t - \pi/4)``
( shm equation ``x(t) = a\sin(\omega t + \alpha)``
comparing with shm,
A= ``\sqrt2`` and Time period T = ``2\pi/\omega`` and phase angle = ``\pi/4`` or ``( 2\pi-\pi/4) = 7\pi/4``.
(2) (3)
(3) 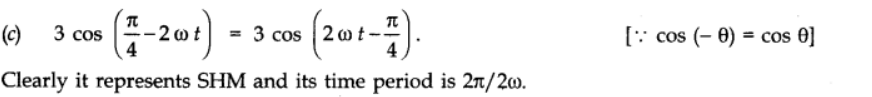
(4) (5) (e) e-w2t2 . It is an exponential function which never repeats itself. Therefore it represents non-periodic motion.
(5) (e) e-w2t2 . It is an exponential function which never repeats itself. Therefore it represents non-periodic motion.
(6) (f) 1 + wt + w2t2 also represents non periodic motion.
- #4-1(a) sin wt - cos wtAns : ``\sin \omega t - \cos \omega t``
=``\sin\omega t - \sin(\pi/2 -\omega t)`` ( as ``cos (\pi/2-\theta) = \sin \theta``)
(Again (`` \sin A - \sin B = 2\sin \frac{A-B}{2} \cos\frac{A+B}{2}``)
=``2 \cos \pi/4 \sin(\omega t - \pi/4)``
= ``\sqrt{2} \sin(\omega t - \pi/4)``
( shm equation ``x(t) = a\sin(\omega t + \alpha)``
comparing with shm,
A= ``\sqrt2`` and Time period T = ``2\pi/\omega`` and phase angle = ``\pi/4`` or ``( 2\pi-\pi/4) = 7\pi/4``.
- #4-2(b) sin3 wtAns :

- #4-3(c) 3 cos -2 cos (``\pi``/4-2 wt)Ans :
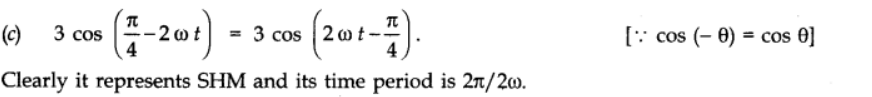
- #4-4(d) cos wt + cos 3 wt + cos 5 wt
Ans :
- #4-5(e) ``e^{-w^2t^2}``Ans : (e) e-w2t2 . It is an exponential function which never repeats itself. Therefore it represents non-periodic motion.
- #4-6(f) 1 + wt + w2t2.Ans : (f) 1 + wt + w2t2 also represents non periodic motion.