35: Magnetic Field Due To A Current : Cbse-xi-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

CBSE-XI-Physics

35: Magnetic Field due to a Current

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #12
Consider a long, straight wire of cross-sectional area A carrying a current i. Let there be n free electrons per unit volume. An observer places himself on a trolley moving in the direction opposite to the current with a speed
v=inAeand separation from the wire by a distance r. The magnetic field seen by the observer is very nearly
(a)
μ0i2πr
(b) zero
(c)
μ0iπr
(d)
2μ0iπr
digAnsr: a
Ans : (a) `` \frac{{\,\mathrm{\,\mu \,}}_{o}i}{2\,\mathrm{\,\pi \,}r}``
Magnetic field will be independent of the motion of the observer because the velocity with which the observer is moving is comparable to drift velocity of electron which is very small as compared to the speed of flow of current from one end of wire to other end. So it can be neglected and hence, magnetic field due to the wire w.r.t the observer will be
B = `` \frac{{\,\mathrm{\,\mu \,}}_{o}i}{2\,\mathrm{\,\pi \,}r}``

Page No 249:

#
Section : iii

Qstn #1
The magnetic field at the origin due to a current element
i dl→placed at a position
r→is
(a)
μ0i4πdl →×r →r3
(b)
-μ0i4πr →×dl →r3
(c)
μ0i4πr →×dl →r3
(d)
-μ0i4πdl →×r →r3
digAnsr: a,b
Ans : (a) `` \frac{{\,\mathrm{\,\mu \,}}_{0}i}{4\pi }\frac{d\stackrel{\to }{l}\times \stackrel{\to }{r}}{{r}^{3}}``
(b) `` -\frac{{\,\mathrm{\,\mu \,}}_{0}i}{4\pi }\frac{\stackrel{\to }{r}\times d\stackrel{\to }{l}}{{r}^{3}}``
The magnetic field at the origin due to current element `` id\stackrel{\to }{l}`` placed at a position `` \stackrel{\to }{r}`` is given by
`` d\stackrel{\to }{B}=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}}{4\,\mathrm{\,\pi \,}}i\frac{\stackrel{\to }{r}\times d\stackrel{\to }{l}}{{r}^{3}}``
`` ``
According to the cross product property,
`` \stackrel{\to }{A}\times \stackrel{\to }{B}=-\stackrel{\to }{B}\times \stackrel{\to }{A}``
`` \Rightarrow d\stackrel{\to }{B}=-\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}}{4\,\mathrm{\,\pi \,}}i\frac{\stackrel{\to }{r}\times \stackrel{\to }{dl}}{{r}^{3}}``
Page No 249:

Qstn #2
Consider three quantities
x=E/B, y=1/μ0ε0and
z=lCR. Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.
(a) x, y have the same dimensions.
(b) y, z have the same dimensions.
(c) z, x have the same dimensions.
(d) None of the three pairs have the same dimensions.
digAnsr: a,b,c
Ans : (a) x, y have the same dimensions.
(b) y, z have the same dimensions.
(c) z, x have the same dimensions.
Lorentz Force:
`` qvB=qE``
`` \Rightarrow \,\mathrm{\,Dimensions\,}\,\mathrm{\,of\,}x=\left[v\right]=\left[\frac{E}{B}\right]=\left[{\,\mathrm{\,LT\,}}^{-1}\right]``
`` y=\frac{1}{\sqrt{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{\,\mathrm{\,\epsilon \,}}_{\,\mathrm{\,o\,}}}}=\sqrt{\frac{4\,\mathrm{\,\pi \,}}{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}}\times \frac{1}{4{\,\mathrm{\,\pi \epsilon \,}}_{\,\mathrm{\,o\,}}}}=\sqrt{\frac{9\times {10}^{9}}{{10}^{-7}}}=3\times {10}^{8}=\,\mathrm{\,c\,}``
`` \Rightarrow \,\mathrm{\,Dimensions\,}\,\mathrm{\,of\,}\,\mathrm{\,y\,}=\left[\,\mathrm{\,c\,}\right]=\left[{\,\mathrm{\,LT\,}}^{-1}\right]``
Time constant of RC circuit = RC so dimensionally [RC] = [T]
`` \Rightarrow z=\left[\frac{l}{\,\mathrm{\,RC\,}}\right]\Rightarrow \left[z\right]=\left[{\,\mathrm{\,LT\,}}^{-1}\right]``
Therefore, x, y and z have the same dimensions.
Page No 249:

Qstn #3
A long, straight wire carries a current along the z-axis, One can find two points in the x-y plane such that
(a) the magnetic fields are equal
(b) the directions of the magnetic fields are the same
(c) the magnitudes of the magnetic fields are equal
(d) the field at one point is opposite to that at the other point.
digAnsr: b,c,d
Ans : (b) the directions of the magnetic fields are the same
(c) the magnitudes of the magnetic fields are equal
(d) the field at one point is opposite to that at the other point.
Consider a current carrying wire lying along x axis.
At any two points on z axis which are at equal distance from the wire,one above the wire and one below the wire,the magnitude of magnetic field will be same and their directions will be opposite to each other.
At any two points on z axis which are at different distances from the wire,one above the wire and other also above the wire,the magnitude of magnetic field will be different and their directions will be same to each other.
Page No 249:

Qstn #4
A long, straight wire of radius R carries a current distributed uniformly over its cross section. T he magnitude of the magnetic field is
(a) maximum at the axis of the wire
(b) minimum at the axis of the wire
(c) maximum at the surface of the wire
(d) minimum at the surface of the wire.
digAnsr: b,c
Ans : (b) minimum at the axis of the wire
(c) maximum at the surface of the wire
A long, straight wire of radius R is carrying current i, which is uniformly distributed over its cross section. According to Ampere's law,
`` \oint \stackrel{\to }{B}.d\stackrel{\to }{l}={\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{\,\mathrm{\,inside\,}}``
`` \,\mathrm{\,At\,}\,\mathrm{\,surface\,},``
`` B\times 2\,\mathrm{\,\pi \,}R={\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}i``
`` \Rightarrow {B}_{\,\mathrm{\,surface\,}}=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}i}{2\,\mathrm{\,\pi \,}R}``
`` \,\mathrm{\,Inside\,},B\times 2\,\mathrm{\,\pi \,}r={\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}i\text{'}\,\mathrm{\,for\,}r<R``
`` ``
Here i^, is the current enclosed by the amperian loop drawn inside the wire.
B_inside will be proportional to the distance from the axis.
On the axis
B =0
The magnetic fields from points on the cross section will point in opposite directions and will cancel each other at the centre.
`` \,\mathrm{\,Outside\,},B\times 2\,\mathrm{\,\pi \,}r={\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}i``
`` \Rightarrow {B}_{\,\mathrm{\,outside\,}}=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}i}{2\,\mathrm{\,\pi \,}r},r>R``
Therefore, the magnitude of the magnetic field is maximum at the surface of the wire and minimum at the axis of the wire.
Page No 249:

Qstn #5
A hollow tube is carrying an electric current along its length distributed uniformly over its surface. The magnetic field
(a) increases linearly from the axis to the surface
(b) is constant inside the tube
(c) is zero at the axis
(d) is zero just outside the tube.
digAnsr: b,c
Ans : (b) is constant inside the tube

(c) is zero at the axis
A hollow tube is carrying uniform electric current along its length, so the current enclosed inside the tube is zero.
According to Ampere's law,
`` \oint \stackrel{\to }{B}.d\stackrel{\to }{l}={\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{\,\mathrm{\,inside\,}}``
`` \,\mathrm{\,Inside\,}\,\mathrm{\,the\,}\,\mathrm{\,tube\,},``
`` \oint \stackrel{\to }{B}.d\stackrel{\to }{l}=0,r<R``
`` \Rightarrow {B}_{\,\mathrm{\,inside\,}}=\,\mathrm{\,Constant\,}``
`` \Rightarrow {B}_{\,\mathrm{\,axis\,}}=0``
`` ``
The magnetic fields from points on the circular surface will point in opposite directions and cancel each other.
`` \,\mathrm{\,Outside\,}\,\mathrm{\,the\,}\,\mathrm{\,tube\,},``
`` B\times 2\,\mathrm{\,\pi \,}r={\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}i``
`` \Rightarrow {B}_{\,\mathrm{\,outside\,}}=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}i}{2\,\mathrm{\,\pi \,}r},r>R``
Page No 249:

Qstn #6
In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero
(a) outside the cable
(b) inside the inner conductor
(c) inside the outer conductor
(d) in between the tow conductors.
digAnsr: a,b
Ans : (a) outside the cable
(b) inside the inner conductor
According to Ampere's law, in a coaxial, straight cable carrying currents i in the inner conductor and -i (equally in the opposite direction) in the outside conductor.
Inside the inner conductor
`` \oint \stackrel{\to }{B}.d\stackrel{\to }{l}={\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{\,\mathrm{\,inside\,}}``
`` \oint \stackrel{\to }{B}.d\stackrel{\to }{l}=0``
`` \Rightarrow B.l=0``
`` \Rightarrow B=0``
`` ``
`` ``
In between the 2 conductors
`` \oint \stackrel{\to }{B}.d\stackrel{\to }{l}={\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}i``
`` \Rightarrow B=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}i}{2\,\mathrm{\,\pi \,}r}``
`` ``
Outside the outer conductor
`` \oint \stackrel{\to }{B}.d\stackrel{\to }{l}={\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}(i-i)``
`` \Rightarrow B=0``
Therefore, the magnetic field is zero outside the cable.
Page No 249:

Qstn #7
A steady electric current is flowing through a cylindrical conductor.
(a) The electric field at the axis of the conductor is zero.
(b) The magnetic field at the axis of the conductor is zero.
(c) The electric field in the vicinity of the conductor is zero.
(d) The magnetic field in the vicinity of the conductor is zero.
digAnsr: b,c
Ans : (b) The magnetic field at the axis of the conductor is zero.

(c) The electric field in the vicinity of the conductor is zero.
As the current is flowing through a conductor so it it is distributed only on the surface of the conductor not in the volume of the cylindrical conductor. It is equivalent to charge distribution on a cylindrical sheet for which electric field inside a conducting cylindrical sheet is always zero.
Magnetic fields at any point inside the conducting cylinder is proportional to the distance from the axis of the cylinder.
At the axis, r = 0. This implies that field will be zero at the axis.
Page No 249:

#
Section : iv

Qstn #1
Using the formula
F →=qv →×B → and B=μ0i2πr, show that the SI units of the magnetic field B and the permeability constant µ₀ may be written as N mA^-1 and NA^-2 respectively.
Ans : Using the relation `` \stackrel{\to }{F}=q\stackrel{\rightharpoonup }{v}\times \stackrel{\to }{B}``, we get
`` B=\frac{F}{qv}``
`` =\frac{F}{Itv}``
`` ``
`` ``
Units of
Force (F) = N
Current (I) = A
Time (T) = s
Velocity (v) = m/s
`` \Rightarrow B=\,\mathrm{\,N\,}/\,\mathrm{\,A\,}-\,\mathrm{\,m\,}``
Now, using the relation `` B=\frac{{\mu }_{0}i}{2\,\mathrm{\,\pi \,}r}``, we get
`` \Rightarrow {\mu }_{0}=B\frac{2\,\mathrm{\,\pi \,}r}{i}=\frac{\,\mathrm{\,N\,}}{\,\mathrm{\,A\,}-\,\mathrm{\,m\,}}\times \frac{\,\mathrm{\,m\,}}{\,\mathrm{\,A\,}}``
`` \Rightarrow {\mu }_{0}\mathit{=}\,\mathrm{\,N\,}/{\,\mathrm{\,A\,}}^{2}``
Page No 249:

Qstn #2
A current of 10 A is established in a long wire along the positive z-axis. Find the magnetic field
B →at the point (1 m, 0, 0).
Ans : Given:
Magnitude of current, I = 10 A
Separation of the point from the wire, d = 1 m

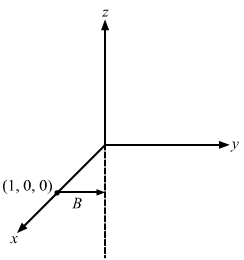
The magnetic field `` \stackrel{\to }{B}`` at point (1 m, 0, 0) is given by
`` B=\frac{{\,\mathrm{\,\mu \,}}_{0}i}{2\,\mathrm{\,\pi \,}d}=\frac{4\,\mathrm{\,\pi \,}\times {10}^{-7}\times 10}{2\,\mathrm{\,\pi \,}\times 1}``
`` \Rightarrow B=2\times {10}^{-6}\,\mathrm{\,T\,}``
(Along the +ve y-axis by the right-hand thumb rule)
Page No 250:

Qstn #3
A copper wire of diameter 1.6 mm carries a current of 20 A. Find the maximum magnitude of the magnetic field
B →due to this current.
Ans : Given:
Magnitude of current, I = 10 A
Diameter of the wire, d = 1.6 × 10^-3 m
∴ Radius of the wire = 0.8 × 10^-3 m
The magnetic field intensity is given by
`` \,\mathrm{\,B\,}=\frac{{\mu }_{0}i}{2\,\mathrm{\,\pi \,}r}``
`` =\frac{2\times {10}^{-7}\times 20}{0.8\times {10}^{-3}}=5\,\mathrm{\,mT\,}``
Page No 250:

Qstn #4
A transmission wire carries a current of 100 A. What would be the magnetic field B at a point on the road if the wire is 8 m above the road?
Ans : Given:
Magnitude of current, I = 100 A
Separation of the road from the wire, d = 8 m
Thus, the magnetic field is given by
`` B=\frac{{\mu }_{0}i}{2\,\mathrm{\,\pi \,}d}=\frac{2\times {10}^{-7}\times 100}{8}=2.5\,\mathrm{\,mT\,}``
Page No 250:

Qstn #5
A long, straight wire carrying a current of 1.0 A is placed horizontally in a uniform magnetic field B = 1.0 × 10^-5 T pointing vertically upward figure. Find the magnitude of the resultant magnetic field at the points P and Q, both situated at a distance of 2.0 cm from the wire in the same horizontal plane.
Figure
Ans : Given:
Uniform magnetic field, B₀ = 1.0 × 10^-5 T (Vertically upwards)
Separation of the point from the wire, d = 2 cm = 0.02 m
The magnetic field due to the wire is given by
`` {B}_{\,\mathrm{\,w\,}}=\frac{{\mu }_{0}i}{2\,\mathrm{\,\pi \,}d}=\frac{4\,\mathrm{\,\pi \,}\times {10}^{-7}\times 1}{2\pi \times 0.02}``
`` \Rightarrow {B}_{\,\mathrm{\,w\,}}=1\times {10}^{-5}\,\mathrm{\,T\,}``

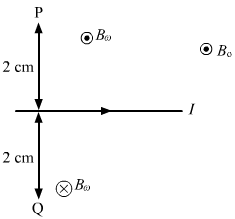
Now,
Net magnetic field at point P:
B_P = B_w+ B₀ = 2 × 10^-5 T
Net magnetic field at point Q:
B_Q = B_w- B₀ = 0
Page No 250: