CBSE-XI-Physics
35: Magnetic Field due to a Current
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #10In order to have a current in a long wire, it should be connected to a battery or some such device. Can we obtain the magnetic due to a straight, long wire by using Ampere’s law without mentioning this other part of the circuit?Ans : We can obtain a magnetic field due to a straight, long wire using Ampere's law by mentioning the current flowing in the wire, without emphasising on the source of the current in the wire. To apply Ampere's circuital law, we need to have a constant current flowing in the wire, irrespective of its source.
Page No 248:
- Qstn #11Quite often, connecting wires carrying currents in opposite directions are twisted together in using electrical appliances. Explain how it avoids unwanted magnetic fields.Ans : Connecting wires carrying currents in opposite directions are twisted together in using electrical appliances.If the wire is twisted, then the resultant fields from consecutive twists are in opposite directions. So the cumulative effect over a long length of wire is roughly zero.
Let at any point in between the two wires, B1 and B2 be the magnetic field due to wire 1 and wire 2 respectively.
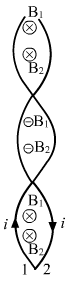
From the diagram, we can see that the net magnetic field due to first turn is into the paper and due to second twisted turn is out of the plane of paper so these fields will cancel each other. Hence if the wire is twisted, then the resultant fields from consecutive twists are in opposite directions. So the cumulative effect over a long length of wire is roughly zero.
Page No 248:
- Qstn #12Two current-carrying wires may attract each other. In absence of other forces, the wires will moves towards each other increasing the kinetic energy. Does it contradict the fact that the magnetic force cannot do any work and hence cannot increase the kinetic energy?Ans : Magnetic field can not do any work and hence can never speed up or down a particle.
Consider 2 wires carrying current in upward direction.
Magnetic field due to current in wire 1 produces a magnetic field out of the plane of paper at the position of wire 2. Due to this magnetic field, a force is exerted on wire 2. Wire 2 electron, moving in downward direction, move in circular paths due to this magnetic force. As these electrons can not come out of the wire so while describing circular path,they hit the edges of the wire and tranfer a momentum to the wire. Due to this change in momentum, wire starts moving and gains kinetic energy.
Page No 248:
- #Section : ii
- Qstn #1A vertical wire carries a current in upward direction. An electron beam sent horizontally towards the wire will be deflected
(a) towards right
(b) towards left
(c) upwards
(d) downwards.digAnsr: cAns : (c) upwards
A vertical wire is carrying current in upward direction, so the magnetic field produced will be anticlockwise (according to the right-hand thumb rule). As the electron beam is sent horizontally towards the wire, the direction of the current will be horizontally away from the wire (direction of conventional current is opposite to the direction of the negative charge). According to Fleming's left-hand rule, the force will act in upward direction, deflecting the beam in the same direction.
Page No 248:
- Qstn #2A current-carrying, straight wire is kept along the axis of a circular loop carrying a current. This straight wire
(a) will exert an inward force on the circular loop
(b) will exert an outward force on the circular loop
(c) will not exert any force on the circular loop
(d) will exert a force on the circular loop parallel to itself.digAnsr: cAns : (c) will not exert any force on the circular loop
The magnetic force on a wire carrying an electric current i is given as `` \stackrel{\to }{F}=i.(\stackrel{\to }{l}\times \stackrel{\to }{B})``, where l is the length of the wire and B is the magnetic field acting on it. If a current-carrying straight wire is kept along the axis of a circular loop carrying current, then according to the right-hand thumb rule, the magnetic field due to the wire on the current-carrying loop will be along its circumference, which contains a current element `` id\stackrel{\to }{l}``.
So, the cross product will be
`` (\stackrel{\to }{l}\times \stackrel{\to }{B})=0``
`` \Rightarrow \stackrel{\to }{F}=0``
Thus, the straight wire will not exert any force on the loop.
Page No 248:
- Qstn #3A proton beam is going from north to south and an electron beam is going from south to north. Neglecting the earth’s magnetic field, the electron beam will be deflected
(a) towards the proton beam
(b) away from the proton beam
(c) upwards
(d) downwards.digAnsr: aAns : (a) towards the proton beam
A proton beam is going from north to south, so the direction of the current due to the beam will also be from north to south. Also, an electron beam is going from south to north, so the direction of the current due to the beam will also be from north to south. The direction of conventional current is along the direction of the flow of the positive charge and opposite to the flow of the negative charge. The magnetic field generated due to them will enter the plane of paper in the west and come out of the plane of paper in the east, according to the right-hand thumb rule. Since both the beams have currents in the same direction, they will apply equal and opposite forces on each other and, hence, will attract each other. Thus, the electron beam will be deflected towards the proton beam.
Page No 248:
- Qstn #4A circular loop is kept in that vertical plane which contains the north-south direction. It carries a current that is towards north at the topmost point. Let A be a point on the axis of the circle to the east of it and B a point on this axis to the west of it. The magnetic field due to the loop
(a) is towards east at A and towards west at B
(b) is towards west at A and towards east at B
(c) is towards east at both A and B
(d) is towards west at both A and BdigAnsr: dAns : (d) is towards west at both A and B
According to the right-hand thumb rule, if we curl the fingers of our right hand in the direction of the current flowing, then the stretching of the thumb will show the direction of the magnetic field developed due to it and vice versa.
Let north-south is along x axis and east-west is along y axis. Circular wire is in xz plane. Then point A will lie on positive y axis and B on negative y axis. On looking from point B, current is flowing in anticlockwise direction so the magnetic field will point from right to left. Hence, the magnetic field due to the loop will be towards west at both A and B.
Page No 248:
- Qstn #5Consider the situation shown in figure. The straight wire is fixed but the loop can move under magnetic force. The loop will
(a) remain stationary
(b) move towards the wire
(c) move away from the wire
(d) rotate about the wire.
FiguredigAnsr: bAns : (b) move towards the wire
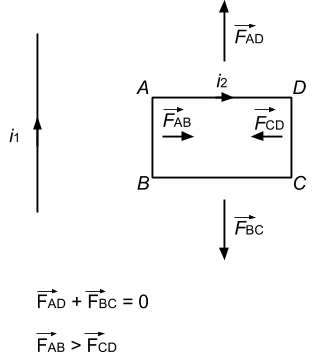
Force acting on the wire per unit length carrying current i2 due to the wire carrying current i1 placed at a distance d is given by
`` F=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{1}{i}_{2}}{2\,\mathrm{\,\pi \,}d}``
So, forces per unit length acting on sides AB and CD are as follows:
`` {F}_{\,\mathrm{\,AB\,}}=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{1}{i}_{2}}{2\,\mathrm{\,\pi \,}d}(\,\mathrm{\,Towards\,}\,\mathrm{\,the\,}\,\mathrm{\,wire\,})``
`` {F}_{\,\mathrm{\,CD\,}}=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{1}{i}_{2}}{2\,\mathrm{\,\pi \,}(d+a)}(\,\mathrm{\,Away\,}\,\mathrm{\,from\,}\,\mathrm{\,the\,}\,\mathrm{\,wire\,})``
Here, FAB > FCD because force is inversly proportional to the distance from the wire and wire AB is closer to the wire carrying current i1.
The forces per unit length acting on sides BC and DA will be equal and opposite, as they are equally away from the wire carrying current i1, with current i2 flowing in the opposite direction.
∴ FBC = `` -``FDA
Now,
Net force:
`` F={F}_{\,\mathrm{\,AB\,}}\mathit{+}{F}_{\,\mathrm{\,BC\,}}\mathit{+}{F}_{\,\mathrm{\,CD\,}}\mathit{+}{F}_{\,\mathrm{\,DA\,}}``
`` \Rightarrow F=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{1}{i}_{2}}{2\,\mathrm{\,\pi \,}d}+{F}_{\,\mathrm{\,BC\,}}-\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{1}{i}_{2}}{2\,\mathrm{\,\pi \,}(d+a)}-{F}_{\,\mathrm{\,BC\,}}``
`` \Rightarrow F=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{1}{i}_{2}}{2\,\mathrm{\,\pi \,}}\left(\frac{1}{d}-\frac{1}{d+a}\right)``
`` \Rightarrow F=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{1}{i}_{2}a}{2\,\mathrm{\,\pi \,}d(d+a)}``
(Towards the wire)
Therefore, the loop will move towards the wire.
Page No 248:
- Qstn #6A charged particle is moved along a magnetic field line. The magnetic force on the particle is
(a) along its velocity
(b) opposite to its velocity
(c) perpendicular to its velocity
(d) zero.digAnsr: dAns : (d) zero
The force on a charged particle q moving with velocity v in a magnetic field B is given by
`` \stackrel{\to }{F}=q(\stackrel{\to }{v}\times \stackrel{\to }{B})``
As the charge is moving along the magnetic line of force, the velocity and magnetic field vectors will point in the same direction, making a cross product.
`` (\stackrel{\to }{v}\times \stackrel{\to }{B})=0``
`` \Rightarrow \stackrel{\to }{F}=0``
So, the magnetic force on the particle will be zero.
Page No 248:
- Qstn #7A moving charge produces
(a) electric field only
(b) magnetic field only
(c) both of them
(d) none of them.digAnsr: cAns : (c) both of them
Because of the presence of a charge, a particle produces an electric field. Also, because of its motion, that is, the flow of charge or current, there is generation of a magnetic field.
Page No 249:
- Qstn #8A particle is projected in a plane perpendicular to a uniform magnetic field. The area bounded by the path described by the particle is proportional to
(a) the velocity
(b) the momentum
(c) the kinetic energy
(d) none of these.digAnsr: cAns : (c) the kinetic energy
When a particle of mass m carrying charge q is projected with speed v in a plane perpendicular to a uniform magnetic field B, the field tends to deflect the particle in a circular path of radius r.
`` \therefore \frac{m{v}^{2}}{r}=qvB``
`` \Rightarrow r=\frac{mv}{qB}``
`` \,\mathrm{\,Now\,},``
`` \,\mathrm{\,Area\,},A=\,\mathrm{\,\pi \,}{r}^{2}``
`` \Rightarrow A=\,\mathrm{\,\pi \,}{\left(\frac{mv}{qB}\right)}^{2}``
`` \Rightarrow A=k{v}^{2}``
`` \,\mathrm{\,Here\,},``
`` k=\,\mathrm{\,\pi \,}{\left(\frac{m}{qB}\right)}^{2}``
`` ``
`` ``
`` ``
Kinetic energy of the particle, `` E=\frac{1}{2}m{v}^{2}``
Therefore, the area bounded is proportional to the kinetic energy.
Page No 249:
- Qstn #9Two particles X and Y having equal charge, after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the mass of X to that of Y is
(a) (R1/R2)1/2
(b) R1/R2
(c) (R1/R2)2
(d) R1R2.digAnsr: cAns : (c)`` \frac{{{R}_{1}}^{2}}{{{R}_{2}}^{2}}``
Particles X and Y of respective masses m1 and m2 are carrying charge q describing circular paths with respective radii R1 and R2 such that
`` {R}_{1}=\frac{{m}_{1}{v}_{1}}{qB}``
`` {R}_{2}=\frac{{m}_{2}{v}_{2}}{qB}``
Since both the particles are accelerated through the same potential difference, both will have the same kinetic energy.
`` \therefore \frac{1}{2}{m}_{1}{{v}_{1}}^{2}=\frac{1}{2}{m}_{2}{{v}_{2}}^{2}``
`` \because {R}_{1}=\frac{{m}_{1}{v}_{1}}{qB}\Rightarrow {v}_{1}=\frac{{R}_{1}qB}{{m}_{1}}``
`` \,\mathrm{\,And\,},``
`` {R}_{2}=\frac{{m}_{2}{v}_{2}}{qB}\Rightarrow {v}_{2}=\frac{{R}_{2}qB}{{m}_{2}}``
`` \therefore {m}_{1}{\left(\frac{{R}_{1}qB}{{m}_{1}}\right)}^{2}={m}_{2}{\left(\frac{{R}_{2}qB}{{m}_{2}}\right)}^{2}``
`` \Rightarrow \frac{{m}_{1}}{{m}_{2}}=\frac{{{R}_{1}}^{2}}{{{R}_{2}}^{2}}``
`` ``
Page No 249:
- Qstn #10Two parallel wires carry currents of 20 A and 40 A in opposite directions. Another wire carying a current anti parallel to 20 A is placed midway between the two wires. T he magnetic force on it will be
(a) towards 20 A
(b) towards 40 A
(c) zero
(d) perpendicular to the plane of the currents.digAnsr: bAns : (b) towards 40 A
According to Fleming's left-hand rule, if the forefinger and middle finger of our left hand point towards the magnetic field acting on a wire and the current flowing in the wire, respectively, then the thumb will point towards the direction in which the force will act (keeping all three perpendicular). Direction of force can be determined using Fleming's left-hand rule.
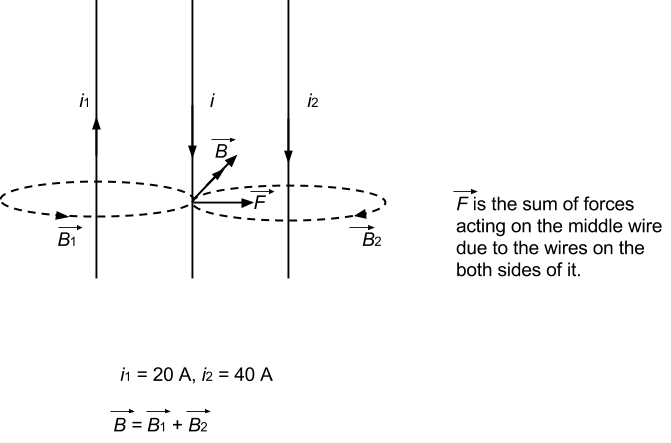
In the figure, dotted circle shows the magnetic filed lines due to both the wires.
Magnetic field at any point on the middle wire will be acting along the tangent to the masgnetic field lines at that point.
Therefore, the wire will experience a magnetic field pointing towards the 40 A wire.
Due to AB, the force will be towards right and due to CD, the force on the wire will be towards right. So, both the forces will add to give a resultant force, which will be towards right, that is, towards the 40 A current-carrying wire.
Page No 249:
- Qstn #11Two parallel, long wires carry currents i1 and i2 with i1 > i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 µT. If the direction of i2 is reversed, the field becomes 30 µT. The ratio i1/i2 is
(a) 4
(b) 3
(c) 2
(d) 1digAnsr: cAns : (c) 2
The magnetic field due to the current-carrying long, straight wire at point a is given by
`` B=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}i}{2\,\mathrm{\,\pi \,}a}``
When both the wires carry currents i1 and i2 in the same direction, they produce magnetic fields in opposite directions at any point in between the wires.
`` B\text{'}=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{1}}{2\,\mathrm{\,\pi \,}a}-\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{2}}{2\,\mathrm{\,\pi \,}a}=10\,\mathrm{\,\mu T\,}..\left(1\right)``
Here, a is the distance of the midpoint from both the wires.
When both the wires carry currents in opposite directions, they produce fields in the same direction at the midpoint of the two wires.
`` B\text{'}\text{'}=\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{1}}{2\,\mathrm{\,\pi \,}a}+\frac{{\,\mathrm{\,\mu \,}}_{\,\mathrm{\,o\,}}{i}_{2}}{2\,\mathrm{\,\pi \,}a}=30\,\mathrm{\,\mu T\,}..\left(2\right)``
On solving eqs. (1) and (2), we get
`` {i}_{1}-{i}_{2}=10``
`` {i}_{1}+{i}_{2}=30``
`` \Rightarrow {i}_{1}=20,{i}_{2}=10``
`` \Rightarrow \frac{{i}_{1}}{{i}_{2}}=\frac{2}{1}=2``
Page No 249: