CBSE-XI-Physics
22: Photometry
- #10A point source of light moves in a straight line parallel to a plane table. Consider a small portion of the table directly below the line of movement of the source. The illuminance at this portion varies with its distance r from the source as
(a) I ∝ ``\frac{1}{r}``
(b) I ∝ ``\frac{1}{r^2}``
(c)I ∝ ``\frac{1}{r^3}``
(d) I ∝ ``\frac{1}{r^4}``digAnsr: CAns : Correct option
(c)
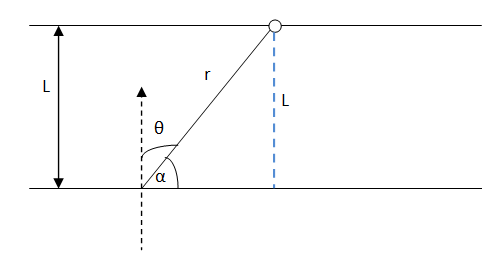
Let the distance between the parallel straight lines be L.
Angle with normal = θ
`` \,\mathrm{\,We\,}\,\mathrm{\,know\,},``
`` I=\frac{{I}_{o}\,\mathrm{\,cos\,}\theta }{{r}^{2}}``
`` \,\mathrm{\,From\,}theabove\,\mathrm{\,fig\,}ure,weget``
`` \,\mathrm{\,I\,}=\frac{{\,\mathrm{\,I\,}}_{\,\mathrm{\,o\,}}\,\mathrm{\,cos\,}\left({90}^{0}-\,\mathrm{\,\alpha \,}\right)}{{\,\mathrm{\,r\,}}^{2}}``
`` \Rightarrow \,\mathrm{\,I\,}=\frac{{\,\mathrm{\,I\,}}_{\,\mathrm{\,o\,}}\,\mathrm{\,sin\alpha \,}}{{\,\mathrm{\,r\,}}^{2}}``
`` \Rightarrow \,\mathrm{\,I\,}=\frac{{\,\mathrm{\,I\,}}_{\,\mathrm{\,o\,}}}{{\,\mathrm{\,r\,}}^{2}}\left(\frac{\,\mathrm{\,L\,}}{\,\mathrm{\,r\,}}\right)``
`` \Rightarrow \,\mathrm{\,I\,}=\frac{{\,\mathrm{\,I\,}}_{\,\mathrm{\,o\,}}\,\mathrm{\,L\,}}{{\,\mathrm{\,r\,}}^{3}}``
`` \,\mathrm{\,L\,}=\,\mathrm{\,constant\,}\,\mathrm{\,for\,}\,\mathrm{\,parallel\,}\,\mathrm{\,moving\,}\,\mathrm{\,source\,}``
`` So,{\,\mathrm{\,I\,}}_{\,\mathrm{\,o\,}}\,\mathrm{\,L\,}=\,\mathrm{\,k\,}\left(\,\mathrm{\,constant\,}\right)``
`` \Rightarrow \,\mathrm{\,I\,}=\frac{\,\mathrm{\,k\,}}{{\,\mathrm{\,r\,}}^{3}}``
`` \Rightarrow \,\mathrm{\,I \alpha \,}\frac{1}{{\,\mathrm{\,r\,}}^{3}}``
Page No 454: