CBSE-XI-Physics
22: Photometry
- #7The intensity produced by a long cylindrical light source at a small distance r from the source is proportional to
(a)``1r^2``
(b)``1r^3``
(c)1r
(d) none of thesedigAnsr: CAns : Correct option
(c).
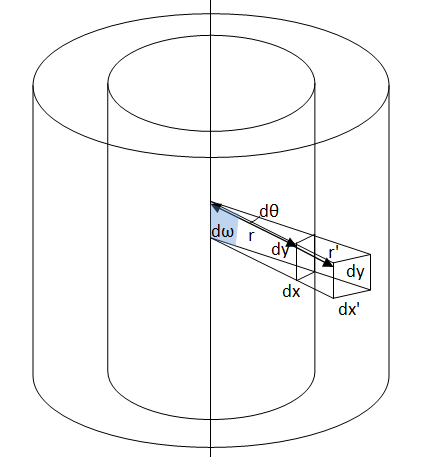
Let us consider two coaxial cylindrical surfaces at distances r and r' from the axis. Let areas dA and dA' subtend the solid angle dω at the central axis. The height of the area element will be same, i.e. equal to dy. Let the breath of dA be dx and that of dA' be dx'.
`` \,\mathrm{\,Now\,}\,\mathrm{\,from\,}\,\mathrm{\,the\,}\,\mathrm{\,arc\,}s,``
`` \,\mathrm{\,dx\,}=\,\mathrm{\,rd\theta \,}``
`` \,\mathrm{\,dx\,}\text{'}=\,\mathrm{\,r\,}\text{'}\,\mathrm{\,d\theta \,}``
`` \,\mathrm{\,Now\,},``
`` \,\mathrm{\,dA\,}=\,\mathrm{\,dxdy\,}=\,\mathrm{\,rd\theta dy\,}``
`` \,\mathrm{\,dA\,}\text{'}=\,\mathrm{\,dx\,}\text{'}\,\mathrm{\,dy\,}=\,\mathrm{\,r\,}\text{'}\,\mathrm{\,d\theta dy\,}``
`` \frac{\,\mathrm{\,dA\,}}{\,\mathrm{\,dA\,}\text{'}}=\frac{\,\mathrm{\,r\,}}{\,\mathrm{\,r\,}\text{'}}``
`` \Rightarrow \frac{\,\mathrm{\,dA\,}}{\,\mathrm{\,r\,}}=\frac{\,\mathrm{\,dA\,}\text{'}}{\,\mathrm{\,r\,}\text{'}}=\,\mathrm{\,d\omega \,}``
`` ``
The luminous flux going through the solid angle dω will be:
dF = Idω
`` \,\mathrm{\,Now\,},``
`` \,\mathrm{\,dF\,}=\,\mathrm{\,I\,}\frac{\,\mathrm{\,dA\,}}{\,\mathrm{\,r\,}}``
`` \,\mathrm{\,If\,}\,\mathrm{\,the\,}\,\mathrm{\,surfaces\,}\,\mathrm{\,are\,}\,\mathrm{\,inclined\,}\,\mathrm{\,at\,}\,\mathrm{\,an\,}\,\mathrm{\,angle\,}\,\mathrm{\,\alpha \,},``
`` \,\mathrm{\,dF\,}=\,\mathrm{\,I\,}\frac{\,\mathrm{\,dAcos\alpha \,}}{\,\mathrm{\,r\,}}``
`` \,\mathrm{\,Now\,},\,\mathrm{\,illuminance\,}\,\mathrm{\,is\,}\,\mathrm{\,defined\,}\,\mathrm{\,as\,}``
`` \,\mathrm{\,E\,}=\frac{\,\mathrm{\,dF\,}}{\,\mathrm{\,dA\,}}=\,\mathrm{\,I\,}\frac{\,\mathrm{\,dAcos\alpha \,}}{\,\mathrm{\,r\,}}``
`` \Rightarrow \,\mathrm{\,E\,}\propto \frac{1}{\,\mathrm{\,r\,}}``
`` ``
Page No 454: