HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
CBSE-XI-Physics

05: Newton's Laws of Motion

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • Qstn #6
    A block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally so that the block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude
    (a) mg
    (b) mg/cosθ
    (c) mg cosθ
    (d) mg tanθ
    digAnsr:   i
    Ans :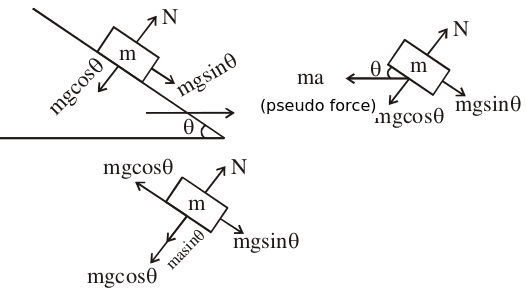 (b) mg/cosθ
    Free-body Diagram of the Small Block of Mass 'm'
    The block is at equilibrium w.r.t. to wedge. Therefore,
    mg sinθ = ma cosθ
    ⇒ a = gtanθ
    Normal reaction on the block is
    N = mg cosθ + ma sinθ
    Putting the value of a, we get:
    N = mg cosθ + mg tanθsinθ
    `` N=mg\,\mathrm{\,cos \,}\theta +mg\frac{\,\mathrm{\,sin \,}\theta }{\,\mathrm{\,cos \,}\theta }\,\mathrm{\,sin \,}\theta N=\frac{mg}{\,\mathrm{\,cos \,}\theta }``
  • Qstn #7
    Neglect the effect of rotation of the earth. Suppose the earth suddenly stops attracting objects placed near its surface. A person standing on the surface of the earth will
    (a) fly up
    (b) slip along the surface
    (c) fly along a tangent to the earth’s surface
    (d) remain standing
    digAnsr:   d
    Ans : (d) remain standing
    If the earth suddenly stops attracting objects placed near its surface, the net force on the person will become zero and according to the first law of motion, the person will remain standing.
  • Qstn #8
    Three rigid rods are joined to form an equilateral triangle ABC of side 1 m. Three particles carrying charges 20 μC each are attached to the vertices of the triangle. The whole system is at rest in an inertial frame. The magnitude of the resultant force on the charged particle at A is
    (a) zero
    (b) 3.6 N
    (c) 3.6√3 N
    (d) 7.2 N
    digAnsr:   a
    Ans : (a) zero
    Using, Fnet = ma,
    a = 0 ⇒ Fnet = 0
    As the whole system is at rest, the resultant force on the charged particle at A is zero.
  • Qstn #9
    A force F1 acts on a particle accelerating it from rest to a velocity v. Force F1 is then replaced by F2 which decelerates the particle to rest.
    (a) F1 must be equal to F2.
    (b) F1 may be equal to F2.
    (c) F1 must be unequal to F2.
    (d) None of these.
    digAnsr:   b
    Ans : (b) F1 may be equal to F2.
    Any force applied in the direction opposite the motion of the particle decelerates it to rest.
  • Qstn #10
    Two objects A and B are thrown upward simultaneously with the same speed. The mass of A is greater than that of B. Suppose the air exerts a constant and equal force of resistance on the two bodies.
    (a) The two bodies will reach the same height.
    (b) A will go higher than B.

    (c) B will go higher than A.
    (d) Any of the above three may happen depending on the speed with which the objects are thrown.
    digAnsr:   b
    Ans : (b) A will go higher than B.
    Let the air exert a constant resistance force = F (in downward direction).
    Acceleration of particle A in downward direction due to air resistance, aA = F/mA.
    Acceleration of particle B in downward direction due to air resistance, aB = F/mB.
    mA > mB
    aA < aB
    `` S=ut+\frac{1}{2}a{t}^{2}``
    `` \,\mathrm{\,So \,},{H}_{A}=ut-\frac{1}{2}({a}_{A}+g){t}^{2}``
    `` {H}_{B}=ut-\frac{1}{2}({a}_{B}+g){t}^{2}``
    `` {H}_{A}>{H}_{B}``
    Therefore, A will go higher than B.
  • Qstn #11
    A smooth wedge A is fitted in a chamber hanging from a fixed ceiling near the earth’s surface. A block B placed at the top of the wedge takes time T to slide down the length of the wedge. If the block is placed at the top of the wedge and the cable supporting the chamber is broken at the same instant, the block will
    (a) take a time longer than T to slide down the wedge
    (b) take a time shorter than T to slide down the wedge
    (c) remain at the top of the wedge
    (d) jump off the wedge
    digAnsr:   c
    Ans : (c) remain at the top of the wedge
    Downward gravitational force will be balanced by the upward pseudo force (because of the motion of the wedge in downward direction). The block will remain at its position, as both the box and the inclined plane are falling with the same acceleration (g).
  • Qstn #12
    In an imaginary atmosphere, the air exerts a small force F on any particle in the direction of the particle’s motion. A particle of mass m projected upward takes time t1 in reaching the maximum height and t2 in the return journey to the original point. Then
    (a) t1 < t2
    (b) t1 > t2
    (c) t1 = t2
    (d) the relation between t1 and t2 depends on the mass of the particle
    digAnsr:   b
    Ans : (b) t1 > t2
    Let acceleration due to air resistance force be a.
    Let H be maximum height attained by the particle.
    Direction of air resistance force is in the direction of motion.
    In the upward direction of motion, `` {a}_{\,\mathrm{\,eff \,}}=\left|g-a\right|``.
    `` {t}_{1}=\sqrt{\frac{2H}{\left|g-a\right|}}...\left(1\right)``
    In the downward direction of motion, `` {a}_{\,\mathrm{\,eff \,}}=g+a``.
    `` {t}_{2}=\sqrt{\frac{2H}{g+a}}...\left(2\right)``
    So, t1 > t2.
  • Qstn #13
    A person standing on the floor of an elevator drops a coin. The coin reaches the floor of the elevator in time t1 if the elevator is stationary and in time t2 if it is moving uniformly. Then
    (a) t1 = t2
    (b) t1 < t2
    (c) t1 > t2
    (d) t1 < t2 or t1 > t2 depending on whether the lift is going up or down.
    digAnsr:   a
    Ans : (a) t1 = t2
    After the coin is dropped, the only force acting on it is gravity, which is same for both the cases.
    So t1 = t2.
  • Qstn #14
    A free
    U238nucleus kept in a train emits an alpha particle. When the train is stationary, a nucleus decays and a passenger measures that the separation between the alpha particle and the recoiling nucleus becomes x at time t after the decay. If the decay takes place while the train is moving at a uniform velocity v, the distance between the alpha particle and the recoiling nucleus at a time t after the decay, as measured by the passenger, is
    (a) x + v t
    (b) x - v t
    (c) x
    (d) depends on the direction of the train
    digAnsr:   c
    Ans : (c) x
    The moving train does not put any extra force on the alpha particle and the recoiling nucleus. So, the distance between the alpha particle and the recoiling nucleus at a time t after the decay, as measured by the passenger, will be same as before, i.e. x.
  • #
    Section : iii
  • Qstn #1
    A reference frame attached to the earth
    (a) is an inertial frame by definition
    (b) cannot be an inertial frame because the earth is revolving around the sun
    (c) is an inertial frame because Newton’s laws are applicable in this frame
    (d) cannot be an inertial frame because the earth is rotating about its axis
    digAnsr:   b,d
    Ans : (b) cannot be an inertial frame because the earth is revolving around the sun
    (d) cannot be an inertial frame because the earth is rotating about its axis
    A reference frame attached to the earth cannot be an inertial frame because the earth is revolving around the sun and also rotating about its axis.
  • Qstn #2
    A particle stays at rest as seen in a frame. We can conclude that
    (a) the frame is inertial
    (b) resultant force on the particle is zero
    (c) the frame may be inertial but the resultant force on the particle is zero
    (d) the frame may be non-inertial but there is a non-zero resultant force
    digAnsr:   c,d
    Ans : (c) the frame may be inertial but the resultant force on the particle is zero
    (d) the frame may be non-inertial but there is a non-zero resultant force
    According to Newton's second law which says that net force acting on the particle is equal to rate of change of momentum ( or mathematically F = ma), so if a particle is at rest then Fnet = ma = m`` \frac{dv}{dt}=m\frac{d\left(0\right)}{dt}=m\times 0=0``.
    Now, if the frame is inertial, then the resultant force on the particle is zero.
    If the frame is non-inertial,
    vector sum of all the forces plus a pseudo force is zero.
    i.e. Fnet ≠ 0.
  • Qstn #3
    A particle is found to be at rest when seen from a frame S1 and moving with constant velocity when seen from another frame S2. Mark out the possible options.
    (a) Both the frames are inertial.
    (b) Both the frames are non-inertial.
    (c) S1 is inertial and S2 is non-inertial.
    (d) S1 is non-inertial and S2 is inertial
    digAnsr:   a,b
    Ans : (a) Both the frames are inertial.
    (b) Both the frames are non-inertial.
    S1 is moving with constant velocity w.r.t frame S2. So, if S1 is inertial, then S2 will be inertial and if S1 is non-inertial, then S2 will be non-inertial.
  • Qstn #4
    The figure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
    (a) AB
    (b) BC
    (c) CD
    (d) DE
    Figure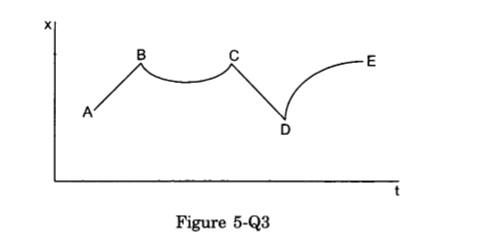
    digAnsr:   a,c
    Ans : (a) AB
    (c) CD
    Slope of the x-t graph gives velocity. In the regions AB and CD, slope or velocity is constant, i.e. acceleration is zero. Hence, from the second law, force is zero in these regions.
  • Qstn #5
    The figure shows a heavy block kept on a frictionless surface and being pulled by two ropes of equal mass m. At t = 0, the force on the left rope is withdrawn but the force on the right end continues to act. Let F1 and F2 be the magnitudes of the forces exerted by right rope and the left rope on the block, respectively.
    Figure
    (a) F1 = F2 = F for t < 0
    (b) F1 = F2 = F + mg for t < 0
    (c) F1 = F, F2 = F for t > 0
    (d) F1 < F, F2 = F for t > 0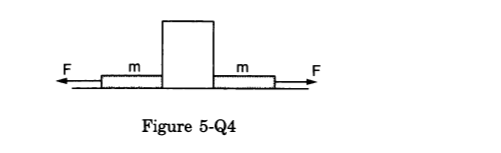
    digAnsr:   a
    Ans : (a) F1 = F2 = F, for t < 0
    At t < 0, the block is in equilibrium in the horizontal direction.
    So, F1 = F2 = F
    At t > 0, F2 = 0 and F1 = F.
    Page No 79:
next page