Qstnid -A-9-let Ε<sub>1</sub> And Ε<sub>2</sub> Be The Angles Made By A→and -A→with The Positive X-axis. Show That Tan Ε<sub>1</sub> = Tan Ε<sub>2</sub><sub>.</sub> Thus, Giving Tan Ε Does Not Uniquely Determine The Direction Of A→. - 02: Physics And Mathematics - Cbse-xi-physics

Home Learn Fast select Course

Show Unit/Chapter Change Unit Change Subject Last Menu

CBSE-XI-Physics

02: Physics and Mathematics

with Solutions -

Qstn# A-9 Prvs-Qstn Next-Qstn

#9
Let ε₁ and ε₂ be the angles made by
A→and
-A→with the positive X-axis. Show that tan ε₁ = tan ε₂_. Thus, giving tan ε does not uniquely determine the direction of
A→.
Ans : The direction of `` -\stackrel{\to }{A}`` is opposite to `` \stackrel{\to }{A}``. So, if vector `` \stackrel{\to }{A}`` and `` -\stackrel{\to }{A}`` make the angles ε₁ and ε₂ with the X-axis, respectively, then ε₁ is equal to ε₂ as shown in the figure:

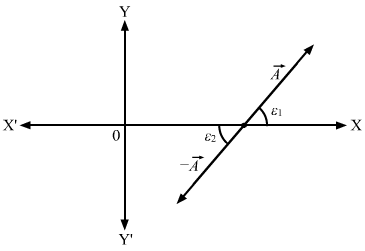
Here, tan ε₁ = tan ε₂
Because these are alternate angles.
Thus, giving tan ε does not uniquely determine the direction of `` \stackrel{\to }{A}``.
Page No 28: