CBSE-XI-Physics
02: Physics and Mathematics
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #Section : APage No 27:
- Qstn #1Is a vector necessarily changed if it is rotated through an angle?Ans : Yes. A vector is defined by its magnitude and direction, so a vector can be changed by changing its magnitude and direction. If we rotate it through an angle, its direction changes and we can say that the vector has changed.
Page No 27:
- Qstn #2Is it possible to add two vectors of unequal magnitudes and get zero? Is it possible to add three vectors of equal magnitudes and get zero?Ans : No, it is not possible to obtain zero by adding two vectors of unequal magnitudes.
Example: Let us add two vectors `` \stackrel{\to }{A}`` and `` \stackrel{\to }{B}`` of unequal magnitudes acting in opposite directions. The resultant vector is given by
`` R=\sqrt{{A}^{2}+{B}^{2}+2AB\mathrm{cos}\theta }
``
If two vectors are exactly opposite to each other, then
`` \theta =180°,\mathrm{cos}180°=-1
R=\sqrt{{A}^{2}+{B}^{2}-2AB}
\Rightarrow R=\sqrt{{\left(A-B\right)}^{2}}
\Rightarrow R=\left(A-B\right)\mathrm{or}\left(B-A\right)``
From the above equation, we can say that the resultant vector is zero (R = 0) when the magnitudes of the vectors `` \stackrel{\to }{A}`` and `` \stackrel{\to }{B}`` are equal (A = B) and both are acting in the opposite directions.
Yes, it is possible to add three vectors of equal magnitudes and get zero.
Lets take three vectors of equal magnitudes `` \stackrel{\to }{A,}\stackrel{\to }{B}\mathrm{and}\stackrel{\to }{C}``, given these three vectors make an angle of `` 120°`` with each other. Consider the figure below:
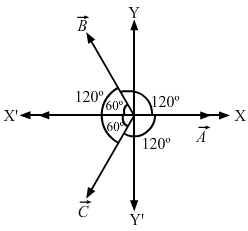
Lets examine the components of the three vectors.
`` {A}_{x}\mathit{=}A
{A}_{y}\mathit{=}0
{B}_{x}\mathit{=}\mathit{-}B\mathrm{cos}60°
{B}_{y}\mathit{=}B\mathrm{sin}\mathit{60}\mathit{°}
{C}_{x}\mathit{=}\mathit{-}C\mathrm{cos}60°
{C}_{y}\mathit{=}\mathit{-}C\mathrm{sin}60°
\mathrm{Here}\mathit{,}\mathit{}A\mathit{=}B\mathit{=}C
\mathrm{So},\mathrm{along}\mathrm{the}x-\mathrm{axis},\mathrm{we}\mathrm{have}:
A\mathit{-}\mathit{(}2A\mathrm{cos}60°\mathit{)}\mathit{=}\mathit{0}\mathit{,}\mathit{}as\mathit{}\mathrm{cos}\mathit{}60°\mathit{=}\frac{\mathit{1}}{\mathit{2}}\mathit{}
\Rightarrow B\mathrm{sin}60°\mathit{-}C\mathrm{sin}60°\mathit{=}\mathit{0}
``
Hence, proved.
Page No 27:
- Qstn #3Does the phrase “direction of zero vector” have physical significance? Discuss it terms of velocity, force etc.Ans : A zero vector has physical significance in physics, as the operations on the zero vector gives us a vector.
For any vector `` \stackrel{\to }{A}``, assume that
`` \stackrel{\to }{A}+\stackrel{\to }{0}=\stackrel{\to }{A}
\stackrel{\to }{A}-\stackrel{\to }{0}=\stackrel{\to }{A}
\stackrel{\to }{A}\times \stackrel{\to }{0}=\stackrel{\to }{0}``
Again, for any real number `` \lambda ``, we have:
`` \lambda \stackrel{\to }{0}=\stackrel{\to }{0}``
The significance of a zero vector can be better understood through the following examples:
The displacement vector of a stationary body for a time interval is a zero vector.
Similarly, the velocity vector of the stationary body is a zero vector.
When a ball, thrown upward from the ground, falls to the ground, the displacement vector is a zero vector, which defines the displacement of the ball.
Page No 27:
- Qstn #4Can you add three unit vectors to get a unit vector? Does your answer change if two unit vectors are along the coordinate axes?Ans : Yes we can add three unit vectors to get a unit vector.
No, the answer does not change if two unit vectors are along the coordinate axes. Assume three unit vectors `` \vec{i,}-\vec{i}\mathrm{and}\vec{j}`` along the positive x-axis, negative x-axis and positive y-axis, respectively. Consider the figure given below:

The magnitudes of the three unit vectors (`` \vec{i,}-\vec{i}\mathrm{and}\vec{j}`` ) are the same, but their directions are different.
So, the resultant of `` \vec{i}\mathrm{and}-\vec{i}`` is a zero vector.
Now, `` \vec{j}+\stackrel{\to }{0}=\vec{j}`` (Using the property of zero vector)
∴ The resultant of three unit vectors (`` \vec{i,}-\vec{i}\mathrm{and}\vec{j}``) is a unit vector (`` \vec{j}``).
Page No 28:
- Qstn #5Can we have physical quantities having magnitude and direction which are not vectors?Ans : Yes, there are physical quantities like electric current and pressure which have magnitudes and directions, but are not considered as vectors because they do not follow vector laws of addition.
Page No 28:
- Qstn #6Which of the following two statements is more appropriate?
.(a) Two forces are added using triangle rule because force is a vector quantity.
(b) Force is a vector quantity because two forces are added using triangle rule.digAnsr: aAns : Two forces are added using triangle rule, because force is a vector quantity. This statement is more appropriate, because we know that force is a vector quantity and only vectors are added using triangle rule.
- Qstn #7Can you add two vectors representing physical quantities having different dimensions? Can you multiply two vectors representing physical quantities having different dimensions?Ans : No, we cannot add two vectors representing physical quantities of different dimensions. However, we can multiply two vectors representing physical quantities with different dimensions.
Example: Torque, `` \stackrel{\to }{\tau }=\stackrel{\to }{r}\times \stackrel{\to }{F}``
Page No 28:
- Qstn #8Can a vector have zero component along a line and still have nonzero magnitude?Ans : Yes, a vector can have zero components along a line and still have a nonzero magnitude.
Example: Consider a two dimensional vector `` 2\vec{i}+0\vec{j}``. This vector has zero components along a line lying along the Y-axis and a nonzero component along the X-axis. The magnitude of the vector is also nonzero.
Now, magnitude of `` 2\vec{i}+0\vec{j}`` = `` \sqrt{{2}^{2}+{0}^{2}}=2``
Page No 28:
- Qstn #9Let ε1 and ε2 be the angles made by
A→and
-A→with the positive X-axis. Show that tan ε1 = tan ε2. Thus, giving tan ε does not uniquely determine the direction of
A→.Ans : The direction of `` -\stackrel{\to }{A}`` is opposite to `` \stackrel{\to }{A}``. So, if vector `` \stackrel{\to }{A}`` and `` -\stackrel{\to }{A}`` make the angles ε1 and ε2 with the X-axis, respectively, then ε1 is equal to ε2 as shown in the figure:
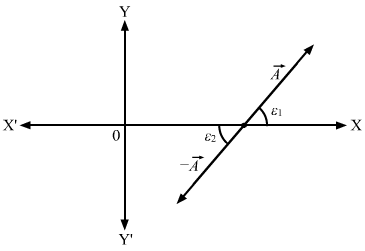
Here, tan ε1 = tan ε2
Because these are alternate angles.
Thus, giving tan ε does not uniquely determine the direction of `` \stackrel{\to }{A}``.
Page No 28:
- Qstn #10Is the vector sum of the unit vectors
i→and
j→a unit vector? If no, can you multiply this sum by a scalar number to get a unit vector?Ans : No, the vector sum of the unit vectors `` \stackrel{\to }{i}`` and `` \stackrel{\to }{j}`` is not a unit vector, because the magnitude of the resultant of `` \stackrel{\to }{i}`` and `` \stackrel{\to }{j}`` is not one.
Magnitude of the resultant vector is given by
R = `` \sqrt{{1}^{2}+{1}^{2}+\mathrm{cos}90°}=\sqrt{2}``
Yes, we can multiply this resultant vector by a scalar number `` \frac{1}{\sqrt{2}}`` to get a unit vector.
Page No 28:
- Qstn #11Let
A→=3i→+4j→. Write a vector
B→such that
A→≠B→, but A = B.Ans : A vector `` \stackrel{\to }{B}`` such that `` \stackrel{\to }{A}\ne \stackrel{\to }{B}``, but A = B are as follows:
`` \left(\mathrm{i}\right)\stackrel{\to }{B}=3\stackrel{\to }{i}-4\stackrel{\to }{j}
\left(\mathrm{ii}\right)\stackrel{\to }{B}=3\stackrel{\to }{j}+4\stackrel{\to }{k}
\left(\mathrm{iii}\right)\stackrel{\to }{B}=3\stackrel{\to }{k}+4\stackrel{\to }{i}
\left(\mathrm{iv}\right)\stackrel{\to }{B}=3\stackrel{\to }{j}-4\stackrel{\to }{k}``
Page No 28:
- Qstn #12Can you have
A→×B→=A→·B→with A ≠ 0 and B ≠ 0? What if one of the two vectors is zero?Ans : No, we cannot have `` \stackrel{\to }{A}\times \stackrel{\to }{B}=\stackrel{\to }{A}·\stackrel{\to }{B}`` with A ≠ 0 and B ≠ 0. This is because the left hand side of the given equation gives a vector quantity, while the right hand side gives a scalar quantity. However, if one of the two vectors is zero, then both the sides will be equal to zero and the relation will be valid.
Page No 28:
- Qstn #13If
A→×B→=0, can you say thatAns : If `` \stackrel{\to }{A}\times \stackrel{\to }{B}=0``, then both the vectors are either parallel or antiparallel, i.e., the angle between the vectors is either `` 0°\mathrm{or}180°``.
(`` \stackrel{\to }{A}\stackrel{\to }{B}\mathrm{sin}\theta \vec{n}=0`` `` \because `` `` \mathrm{sin}0°=\mathrm{sin}180°=0``)
Both the conditions can be satisfied: