Previous Year Paper year:2012 : ICSE-X-Mathematics

Change Unit Change Subject Last Menu

ICSE-X-Mathematics

Previous Year Paper year:2012

with Solutions -

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#
ICSE X | Mathematics
Board Paper . 2012
ICSE Board
Class X Mathematics
Board Question Paper 2012
(Two and a half hours)
Answers to this Paper must be written on the paper provided separately.
You will not be allowed to write during the first 15 minutes.
This time is to be spent in reading the Question Paper.
The time given at the head of this Paper is the time allowed for writing the answers.
Attempt all questions from Section A and any four questions from Section B.
All working, including rough work, must be clearly shown and must be done on the same
sheet as the rest of the answer.
Omission of essential working will result in loss of marks.
The intended marks for questions or parts of questions are given in brackets [ ].
Mathematical tables are provided.

# [40]
Section : A
Attempt all questions from this Section.

#1

#1-a [3]
If A =
\begin{bmatrix} 3 & 1 \\ -1 & 2 \\\end{bmatrix}
and I =
\begin{bmatrix} 1 & 0 \\0 & 1 \\\end{bmatrix},
find ``A^2 - 5A + 7I``.
Ans : Given ``A = \begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}, I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}``
``A^2 - 5A + 7I``
``= \begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} . \begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}- 5. \begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} + 7.\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}``
``= \begin{bmatrix} 9-1 & 3+2 \\ -3-2 & -1+4 \end{bmatrix} - \begin{bmatrix} 15 & 5 \\ -5 & 10 \end{bmatrix} + \begin{bmatrix} 7 & 0 \\ 0 & 7 \end{bmatrix}``
``= \begin{bmatrix} 8 & 5 \\ -5 & 3 \end{bmatrix} - \begin{bmatrix} 15 & 5 \\ -5 & 10 \end{bmatrix} + \begin{bmatrix} 7 & 0 \\ 0 & 7 \end{bmatrix} ``
``= \begin{bmatrix} 8-15+7 & 5-5+0 \\ -5-5+0 & 3-10+7 \end{bmatrix} ``
``= \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}``
= 0

#1-b [3]
The monthly pocket money of Ravi and Sanjeev are in the ratio 5:7. Their
expenditures are in the ratio 3:5. If each saves Rs. 80 every month, find their
monthly pocket money.
Ans : Let monthly pocket money be Ravi is 5x and Sanjeev is 7x .
They both save ``Rs. \ 80`` per month.
Therefore, their expenditure would be (5x-80) and (7x -80) respectively.
Hence ``\frac{5x-80}{7x-80} = \frac{3}{5}``
``\Rightarrow 25x - 400 = 21x -240``
``\Rightarrow x = 40 \ Rs. ``
Ravi.s pocket money = 5x = ``200 \ Rs. ``
Sanjeev.s pocket money ``= 7x = 280 \ Rs. ``

#1-c [4]
Using the Remainder Theorem factorise completely the following polynomial.
``3x^3 + 2x^2 - 19x + 6``
Ans : Given ``f(x)=3x^3+ 2x^2-19x+6``
Try ``x = 1, f(1)=3+2-19+6=0 ``
``f(1)=-3+2+19+6 \neq 0`` , therefore (x-1) is not a factor of the given function.
Try ``x = 2, f(2)=24+8-38+6=0 ``
Therefore (x-2) is a factor of f(x)
``x-2 ) \overline {3x^3+ 2x^2-19x+6} (3x^2+8x-3
(-) \ \ \underline {3x^3-6x^2}
8x^2-19x+6
(-) \ \ \underline{8x^2-16x}
{ -3x+6}
(-) \ \ \underline{ -3x+6}
\times ``
To factories ``3x ^2+8x-3``
``3x ^2+8x-3 = 3x ^2+9x-x-3``
``=3x(x+3)-1(x+3) ``
``=(3x-1)(x+3) ``
Hence, ``3x ^3+ 2x ^2-19x+6=(x-2)(3x-1)(x+3)``

#2

#2-a [3]
On what sum of money will the difference between the compound interest and
simple interest for 2 years be equal to Rs. 25 if the rate of interest charged for both
is 5% p.a.?
Ans : Let the sum be ``x \ Rs``.
Simple Interest for 2 years ``= x \times \frac{5}{100} \times 2 = 0.1x ``
Amount Compound Interest
``A=P(1+\frac{r}{100})^n \Rightarrow A = x(1+\frac{5}{100})^2 \Rightarrow A = 1.1025x \ Rs.``
Given difference = 25 Rs.
Therefore C.I. - S.I. ``= 25 \Rightarrow (1.1025x-x)-(0.1x) = 25 \Rightarrow x = 10000 \ Rs. ``

#2-b [3]
ABC is an isosceles right angled triangle with ∠ABC = 90°. A semi-circle is drawn
with AC as the diameter. If AB = BC = 7 cm, find the area of the shaded region.

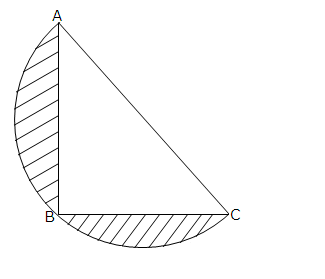
Take ``\pi = \frac{22}{7}``
Ans : ``\triangle ABC`` is a right angled triangle. Therefore
``AC^2 = AB^2+BC^2 = (7)^2 + (7)^2 = 98 ``
``\Rightarrow AC = 7 \sqrt{2} ``
Area of semi circle ``= \frac{1}{2} \times \frac{22}{7} \times (\frac{7 \sqrt{2}}{2})^2 = 38.5 cm^2``
Area of ``\triangle ABC = \frac{1}{2} \times 7 \times 7 = 24.5 cm^2 ``
Area of the shaded region = Area of the semi circle . Area of ``\triangle ABC = 38.5 - 24.5 = 14 cm^2``

#2-c
Given a line segment AB joining the points A(-4, 6) and B(8, -3). Find
Ans : Let the required ratio be k: 1 and the point of intersection y-axis be (0, y)
Since ``x = \frac{kx_2+x_1}{k+1} ``
``\Rightarrow 0 = \frac{k \times (8)-4}{k+1} ``
``\Rightarrow 8k-4=0 ``
``\Rightarrow k = \frac{1}{2} ``
``\Rightarrow m_1:m_2 = 1:2 ``
``y = \frac{1 \times (-3)+2 \times (6)}{ 1+2} = 3 ``
Therefore the point intersection is = (0, 3)
Length of ``AB = \sqrt{(8-(-4))^2+(-3-6)^2} = \sqrt{144+81} = \sqrt{225} = 15 \ units`` .

#2-c-i
The ratio in which AB is divided by y-axis.

#2-c-ii
Find the coordinates of the point of intersection.

#2-c-iii [4]
The length of AB.

#3

#3-a [3]
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm
and AC = 7.5 cm. Calculate the radius of circle.

Ans : Let the radius of the circle = r
Here we apply intercept theorem. Therefore:
``AC \times AD = AB^2 ``
``7 \times (7.5 + 2r ) = 15^2 ``
``2r = 30-7.5 = 22.5 \Rightarrow r = 11.25 \ cm ``