Previous Year Paper year:2012 : ICSE-X-Mathematics

Change Unit Change Subject Last Menu

ICSE-X-Mathematics

Previous Year Paper year:2012

with Solutions - page 2

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#3-b [3]
Evaluate without using trigonometric tables:
$$\cos^2 26° + \cos^2 64° sin 26° + \frac{tan36°}{cot54°}$$
Ans : ``cos^2 \ 26° + cos \ 64°.sin \ 26° + \frac{tan \ 36°}{cot \ 54°}``
``= cos^2 \ 26° + cos \ (90° - 26°).sin \ 26° + \frac{tan \ (90° - 54°)}{cot \ 54°} ``
``= cos^2 \ 26° + sin^2 \ 26° + \frac{cot \ 54°}{cot \ 54°} ``
= 2

#3-c [4]
Marks obtained by 40 students in a short assessment is given below, where a and b
are two missing data.

Marks 5 6 7 8 9
Number of Students 6 a 16 13 b

If the mean of the distribution is 7.2, find a and b.
Ans : Given, the total number of students = 40
Therefore 6 + a+ 16+ 13+ b = 40
``\Rightarrow a + b = 5 . . . (i)``
Given ``mean (\overline{x}) = \frac {\Sigma fx}{\Sigma f} = 7.2 ``
Therefore ``7.2 = \frac{5 \times 6 + 6 \times a +7 \times 16 +8 \times 13 +9 \times b}{40} ``
246 + 6a + 9 b = 288
6a + 9 b = 42
2a + 3b = 14 . . . (ii)
Solving (i) and (ii) we get a = 1 and b = 4

#4

#4-a [3]
Kiran deposited Rs. 200 per month for 36 months in a bank.s recurring deposit
account. If the bank pays interest at the rate of 11% per annum, find the
amount she gets on maturity.
Ans : ``P = Rs. \ 200, \ no \ of \ months = 36, \ r = 11\%``
Maturity ``\ Value = P \times n + P \times \frac{n(n+1)}{2 \times 12} \times \frac{r}{100}``
``=200 \times 36 +200 \times \frac{36(36+1)}{2 \times 12} \times \frac{11}{100} = Rs. 8421 ``

#4-b
Two coins are tossed once. Find the probability of getting
Ans : Let Heads . H and Tails . T
If two coins are tossed once, then the total number of possibilities would be as shown: Sample Space (S) = {HH, HT, TH, TT}
n (S) = 4 (i.e. there are 4 possible outcomes)

#4-b-i [3]
2 heads (ii) at least 1 tail.
Ans : Event: getting two heads ``= {HH} \Rightarrow n(E) = 1 ``
Hence the probability ``P(E) = \frac{n(E)}{n(S)} = \frac{1}{4} = 0.25 ``

#4-c
Using graph paper and taking 1 cm = 1 unit along both x-axis and y-axis.
Ans : (i) Please refer to the graph shown below

#4-c-i
Plot the points A(-4, 4) and B(2, 2).

#4-c-ii
Reflect A and B in the origin to get the images A. and B. respectively.
Ans : Please refer to the graph shown below

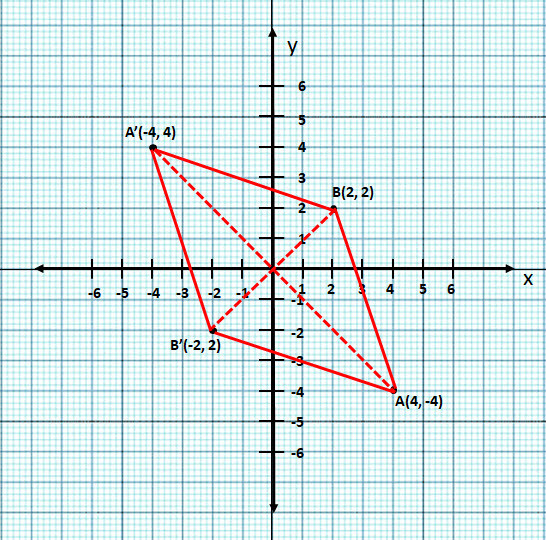
#4-c-iii
Write down the co-ordinates of A. and B..
Ans : Reflection of ``A \ and \ B`` in the origin are ``A'(4, -4) \ and \ B'(-2, -2)`` respectively.

#4-c-iv
Give the geometrical name for the figure ABA.B..
Ans : Name of the geometrical figure in the graph show is Rhombus

#4-c-v [4]
Draw and name its lines of symmetry.
Ans : Two lines of symmetry: Both diagonal ``AA' \ and \ BB'``

# [40]
Section : B
Attempt any four questions from this Section

#5

#5-a [3]
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:

Ans :