Previous Year Paper year:2019 : ICSE-X-Mathematics

Change Unit Change Subject Last Menu

ICSE-X-Mathematics

Previous Year Paper year:2019

with Solutions - page 4

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

No item to list.

Note: Please signup/signin free to get personalized experience.

#6-b
The first and last term of a Geometrical Progression (G.P.) are 3 and 96 respectively. If the

common ratio is 2, find :

Ans : Given that, a = 3 anda_n = 96, r = 2

#6-b-i
‘n’ the number of terms of the G.P.

#6-b-ii
Sum of the n terms.

#6-c
A hemispherical and conical hole is scooped out of a solid wooden cylinder.

Find the volume of the remaining solid where the measurements are as follows :
[4]

The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm. Give your answer correct to the nearest whole number. Take ``\pi`` = ``\frac{22}{7}``

Ans : Given that :

Radius of each of hemisphere, cone and cylinder (r) = 3 cm

Height of cylinder = 7 cm

Height of cone = 3 cm

Volume of remaining solid = Vol. of cylinder - Vol. of cone - Vol. of hemisphere

#7

#7-a
In the given figure, AC is a tangent to the circle with centre 0.

If ∠ADB = 55°, find x and y. Give reasons for your answers.
[3]

Ans : We know that angle between the radius and the tangent at the point of contact is right angle.

#7-b
The model of a building is constructed with the scale factor 1:30.
[3]

Ans : Here, scale factor (k) = ``\frac{1}{30}``

#7-b-i
If the height of the model is 80 cm, find the actual height of the building in metres.

Ans : Height of the model = k(Actual height of the building)

⇒ 80 cm = ``\frac{1}{30}`` (Actual height of the building)

⇒ Actual height of the building = 30 × 80 = 2400 cm

#7-b-ii
If the actual volume of a tank at the top of the building is 27 m, find the volume of the tank on the top of the model.
Ans : Volume of the tank at the top of the model

= k³(Actual volume of the tank)

⇒ Volume of the tank at the top of the model

#7-c
Given , 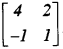M = 6I, where M is a matrix and I is unit matrix of order 2 x 2.
Ans : Here,

∴ The order of matrix M = 2 × 2

#7-c-i
State the order of matrix M.

#7-c-ii
Find the matrix M.
[4]

#8

#8-a
The sum of the first three terms of an Arithmetic Progression (A:P.) is 42 and the product of the first and third term is 52. Find the first term and the common difference.
[3]

Ans : Let the first three terms of an A.P. be a - d, a and a + d.

According to the statement, we have

a - d + a + a + d = 42

3a = 42

a = 14

Now,(a - d)(a + d) = 52

a²- d² = 52

14²- d² = 52

⇒ d² = 196 - 52 = 144

⇒ d = ∓ 12

Hence, the first term is 14 and common difference is ∓ 12.

#8-b
The vertices of a ∆ABC are A(3, 8), B(-1, 2) and C(6, -6). Find :
[3]

Ans : Vertices of a ∆ABC are A(3, 8), B(-1, 2) and C(6, -6)

Slope of the line perpendicular to BC = ``\frac{7}{8}``

Now, equation of the line perpendicular to BC and passing through A is

8y - 64 = 7x - 21

7x - 8y + 43 = 0

(C) Steps of Construction :

1. Draw a line segment BC = 7 cm.

2. Draw its perpendicular bisector 1 and let it intersect BC in M.

3. With M as centre and radius equal to BM or CM, draw a semi-circle and let the semi-circle intersect the perpendicular bisector of line segment BC in A. Join BA.

4. Draw the angle bisector of ∠ABC and let it intersect the semi-circle in D.

5. Join AD and CD.

Hence, ∠ADC = 135°