Previous Year Paper year:2019 : ICSE-X-Mathematics

Change Unit Change Subject Last Menu

ICSE-X-Mathematics

Previous Year Paper year:2019

with Solutions - page 5

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

No item to list.

Note: Please signup/signin free to get personalized experience.

#8-b-i
Slope of BC.

#8-b-ii
Equation of a line perpendicular to BC and passing through A.

#8-c
Using ruler and a compass only construct a semi-circle with diameter BC = 7 cm. Locate a

point A on the circumference of the semicircle such that A is equidistant from B and C. Complete the cyclic quadrilateral ABCD, such that D is equidistant from AB and BC. Measure ∠ADC and write it down.
[4]

#9
Ans :

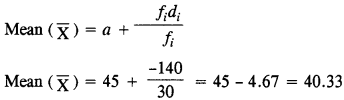
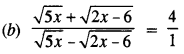
Applying componendo and dividendo, we have

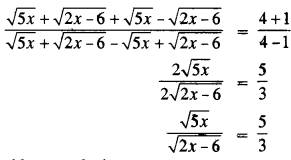
Squaring both sides, we obtain

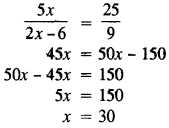
(C) Total investment = ₹ 8500

Market value of each share = ₹ 170

Number of shares purchased = ``\frac{8500}{170}`` = 50

Dividend received = ₹ ``\frac{10}{100}``× 50× 100 = ₹ 500

Now, market value of each share = ₹ (170 + 30) = ₹ 200

Amount received on selling = ₹ (50 x 200) = ₹ 10000

Market value of new shares = ₹ 125 each

Number of shares purchased = ``\frac{10000}{125}`` = 80

Dividend received = ``\frac{12}{100}``× 80×100 = ₹960

Change in income = ₹ (960 - 500)

= ₹ 460

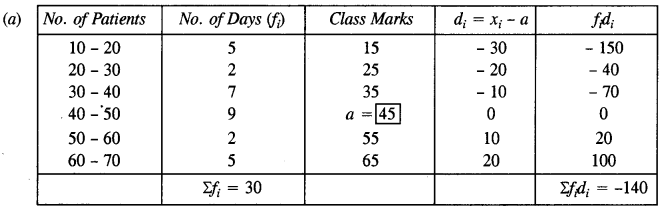
#9-a
The data on the number of patients attending a hospital in a month are given below.
[3]

Find the average (mean) number of patients attending the hospital in a month by using the shortcut method.

Take the assumed mean as 45. Give your answer correct to 2 decimal places.

#9-b
Using properties of proportion solve for x, given
[3]

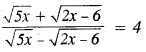
#9-c
Sachin invests ₹ 8500 in 10%, ₹ 100 shares at ₹ 170. He sells the shares when the price of each share rises by ₹ 30 He invests the proceeds in 12% ₹ 100 shares at ₹ 125. Find :

#9-c-i
the sale proceeds.
[4]

#9-c-ii
the number of ₹ 125 shares he buys.

#9-c-iii
the change in his annual income.

#10

#10-a
Use graph paper for this question.
[6]

The marks obtained by 120 students in an English test are given below :

Draw the ogive and hence, estimate :

Ans :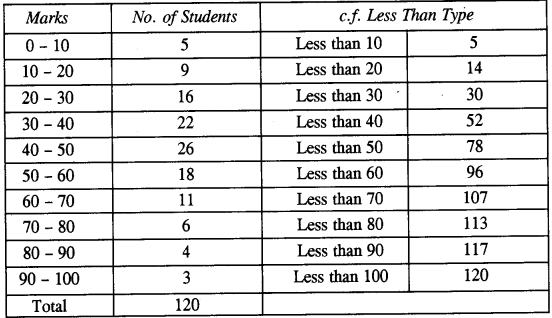

Plot the points (10, 5), (20, 14), (30, 30), (40, 52), (50, 78), (60, 96), (70, 107), (80, 113), (90, 117), (100, 120). On the graph paper by taking upper limits on x-axis and number of students on y-axis. Join them free hand to get smooth curve.

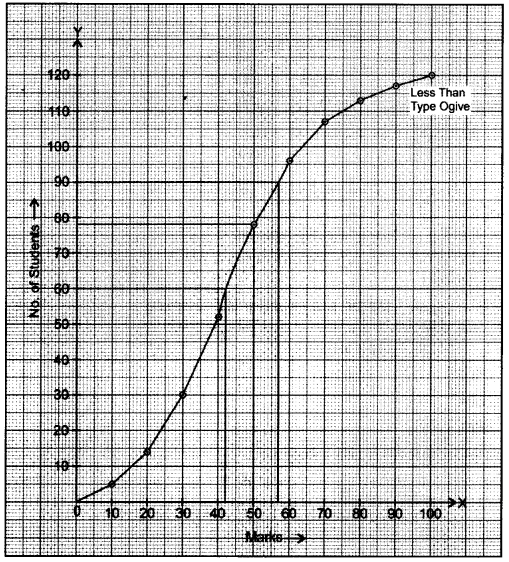
Here, N = 120

``\frac{N}{2}`` = ``\frac{120}{2}`` = 60

Median marks = 42 marks

Number of students who did not pass = 78 students

Upper quartile marks = 57 marks

#10-a-i
the median marks.

#10-a-ii
the number of students who did not pass the test if the pass percentage was 50.

#10-a-iii
the upper quartile marks.