Change UnitChange SubjectLast Menu
ICSE-X-Mathematics

Previous Year Paper year:2019

with Solutions -

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

No item to list.

Note: Please signup/signin free to get personalized experience.

  
  • #
    Answers to this Paper must be written on the paper provided separately.
  • You will not be allowed to write during the first 15 minutes.
  • This time is to be spent in reading the question paper.
  • The time given at the head of this Paper is the time allowed for writing the answers.
  • Attempt all questions from Section A and any four questions from Section B.
  • All working, including rough work, must be clearly shown and must be done on the same sheet as the rest of
  • the answer. Omission of essential working will result in the loss of marks.
  • The intended marks for questions or parts of questions are given in brackets
    [ ].
  • Mathematical tables are provided.


  • #
    Section : A
    [40 marks]

    (Answer all questions from this Section.)
  • #1
    Ans :

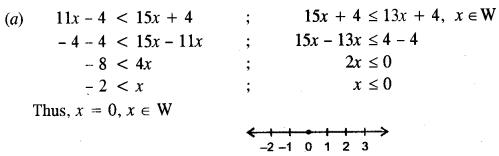
    Total investment = ₹ 4500

    Face value of a share = ₹ 100

    Discount = 10%

    ∴ Market value of a share = ₹ (100 - 10) = ₹ 90

    Now, Number of shares purchased = ``\frac{4500}{90}=50``

    Annual income =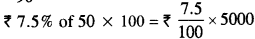

    = ₹ 375



    Here,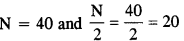

    Marks corresponding to cumulative frequency 20 is 6

    Thus, the required median is 6.

    Clearly, 6 occurs 10 times which is maximum.

    Hence, mode is 6.
  • #1-a
    Solve the following in equation and write down the solution set :
    [3]

    11x - 4 < 15x + 4 ≤ 3x + 14, x ∈ W

    Represent the solution on a real number line.
  • #1-b
    A man invests 4500 in shares of a company which is paying 7.5% dividend.
    [3]

    If 100 shares are available at a discount of 10%. Find :
  • #1-b-i
    Number of shares he purchases.
  • #1-b-ii
    His annual income.
  • #1-c
    In a class of 40 students, marks obtained by the students in a class test (out of 10) are given below :
    [4]



    Calculate the following for the given distribution :
  • #1-c-i
    Median
  • #1-c-ii
    Mode
  • #2
  • #2-a
    Using the factor theorem, show that (x - 2) is a factor of x3+ x2 - 4x - 4.
    [3]

    Hence, factorise the polynomial completely.
    Ans : Given polynomial is p(x) = x3 + x2 - 4x - 4

    x - 2 is its factor, if p(2) = 0

    p(2) = (2)3 + (2)2 - 4(2) - 4 = 8 + 4 - 8 - 4 = 0

    Thus, x - 2 is a factor of p(x).

    Now, x3 + x2 - 4x + 4 = x2(x +1) - 4(x + 1)

    = (x + 1) (x2 - 4)

    = (x + 1) (x + 2) (x - 2)

    Hence, the required factors are (x + 1), (x + 2) and (x - 2).

    L.H.S. = (cosec θ - sin θ) (sec θ - cos θ) (tan θ + cot θ)





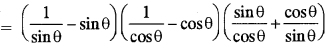
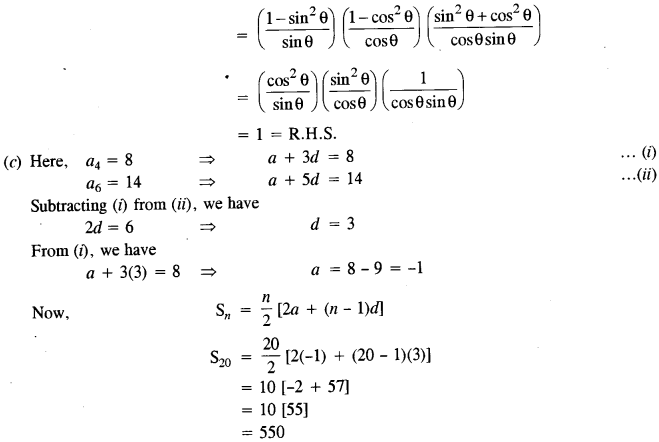
    Hence, first term is - 1, common difference is 3 and sum of the first 20 terms is 550.
  • #2-b
    Prove that :

    (cosec θ - sin θ) (sec θ - cos θ) (tan θ + cot θ) = 1
    [3]
  • #2-c
    In an Arithmetic Progression (A.P.) the fourth and sixth terms are 8 and 14 respectively.

    Find the :
    [4]
  • #2-c-i
    first term
next page