Previous Year Paper year:2019 : ICSE-X-Mathematics

Change Unit Change Subject Last Menu

ICSE-X-Mathematics

Previous Year Paper year:2019

with Solutions - page 2

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

No item to list.

Note: Please signup/signin free to get personalized experience.

#2-c-ii
common difference

#2-c-iii
sum of the first 20 terms.

#3

#3-a
Simplify :

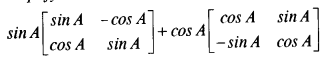
Ans :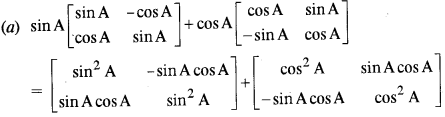

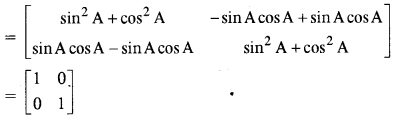
#3-b
M and N are two points on the X axis and Y axis respectively.
[3]

P(3, 2) divides the line segment MN in the ratio 2 : 3.

Find :

Ans : Let the coordinates of M and N be (x, 0) and (0, y)

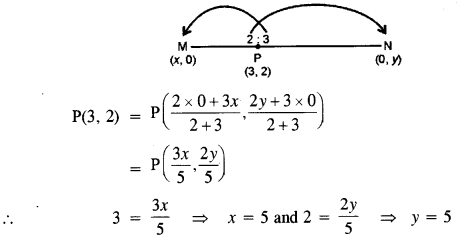
Thus, the coordinates of M and N are M(5,0) and N(0, 5).

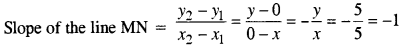
Hence, the slope of the line MN is - 1.

#3-b-i
the coordinates of M and N

#3-b-ii
slope of the line MN.

#3-c
A solid metallic sphere of radius 6 cm is melted and made into a solid cylinder of height 32 cm. Find the :
[4]

Ans : Radius of metallic sphere (R) = 6 cm

Height of cylinder (h) = 32 cm

Volume of cylinder = Volume of metallic sphere

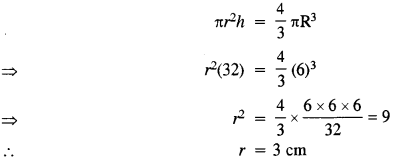
Curved Surface area of the year = 2``\pi``rh

= 2× 3.1 × 3 × 32 = 595.2 cm²

#3-c-i
radius of the cylinder

#3-c-ii
curved surface area of the cylinder

Take ``\pi`` = 3.1

#4

#4-a
The following numbers, K + 3, K + 2, 3K - 7 and 2K - 3 are in proportion. Find K.
[3]

Ans : Here, ``\frac{K+3}{K+2}=\frac{3 K-7}{2 K-3}``

⇒ (K + 3) (2K - 3) = (K + 2) (3K - 7).

⇒ 2K² - 3K + 6K - 9 = 3K²- 7K + 6K - 14

⇒ K² - 4K - 5 = 0

⇒ (K - 5) (K + 1) = 0

⇒ K = 5 or K = - 1

#4-b
Solve for x the quadratic equation x² - 4x - 8 = 0

Give your answer correct to three significant figures.

Ans : Given quadratic equation is x² - 4x - 8 = 0

By using quadratic formula, we have

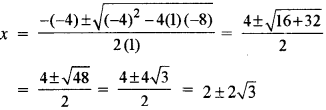
= ``2(1 \pm \sqrt{3})=2(1 \pm 1.73205)=2(2.73205) \text { or } 2(-0.73205)``

= 5.46410 or - 1.4641

= 5.46 or - 1.46

#4-c
Use ruler and compass only for answering this question.
[4]

Draw a circle of radius 4 cm. Mark the center as 0. Mark a point P outside the circle at a distance of 7 cm from the center. Construct two tangents to the circle from the external point P. Measure and write down the length of any one tangent

Ans : Steps of Construction :

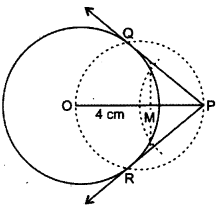
1. Draw a circle of radius 4 cm and centre 0.

2. Draw a radius and produce it to P, such that

OP = 7 cm.

3. Bisect OP at M.

4. With M as centre and MP as radius, draw a circle to intersect the given circle at Q and R.

-5. Join PQ and PR.

PQ and PR are the required tangents and length of the tangents is 5.74 cm.

#
Section : B
[40 Marks]

(Attempt any four questions)