From a disc of radius R and mass M, a circular hole
of diameter R, whose rim passes through the centre
is cut. What is the moment of inertia of the
remaining part of the disc about a perpendicular
axis, passing through the centre ?
(1) 15 ``MR^2``/32
(2) 13 ``MR^2``/32
(3) 11 ``MR^2``/32
(4) 9 ``MR^2``/32

A square loop ABCD carrying a current i, is placed
near and coplanar with a long straight conductor
XY carrying a current I, the net force on the loop
will be :-

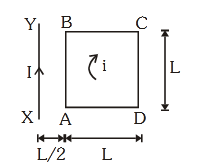
(1) ``\frac {2\mu_0 Ii}{3\pi}``
(2)``\frac {\mu_0 Ii}{2\pi}``
(3) ``\frac {2\mu_0 IiL}{3\pi}``
(4)``\frac {\mu_0 IiL}{2\pi}``

The magnetic susceptibility is negative for :
(1) diamagnetic material only
(2) paramagnetic material only
(3) ferromagnetic material only
(4) paramagnetic and ferromagnetic materials

A siren emitting a sound of frequency 800 Hz
moves away from an observer towards a cliff at a
speed of 15 m/s. Then, the frequency of sound
that the observer hears in the echo reflected from
the cliff is :
(Take velocity of sound in air = 330 m/s)
(1) 765 Hz
(2) 800 Hz
(3) 838 Hz
(4) 885 Hz

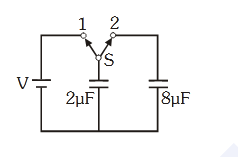
A capacitor of 2µF is charged as shown in the
diagram. When the switch S is turned to position
2, the percentage of its stored energy dissipated is:
(1) 0%
(2) 20%
(3) 75%
(4) 80%

In a diffraction pattern due to a single slit
of width 'a', the first minimum is observed at
an angle 30° when light of wavelength 5000 Å is
incident on the slit. The first secondary maximum
is observed at an angle of :
(1) ``sin^{-1}(\frac 14)``
(2) ``sin^{-1}(\frac 23)``
(3)``sin^{-1}(\frac 12)``
(4) ``sin^{-1}(\frac 34)``

At what height from the surface of earth the
gravitation potential and the value of g are
-5.4 × ``10^7 J kg^{-2}`` and ``6.0 ms^{-2}`` respectively ?
Take the radius of earth as 6400 km :
(1) 2600 km
(2) 1600 km
(3) 1400 km
(4) 2000 km

Out of the following options which one can be used
to produce a propagating electromagnetic wave ?
(1) A charge moving at constant velocity
(2) A stationary charge
(3) A chargeless particle
(4) An accelerating charge

Two identical charged spheres suspended from a
common point by two massless strings of lengths
l, are initially at a distance d (d << l ) apart because
of their mutual repulsion. The charges begin to leak
from both the spheres at a constant rate. As a result,
the spheres approach each other with a
velocity v. Then v varies as a function of the
distance x between the spheres, as :
(1)V ``\propto `` ``X^{\frac 12}``
(2)V ``\propto `` X
(3)V ``\propto `` ``X^{-\frac 12}``
(4) V ``\propto `` ``X^{-1}``

A uniform rope of length L and mass ``m_1`` hangs
vertically from a rigid support. A block of mass
``m_2`` is attached to the free end of the rope.
A transverse pulse of wavelength ``\lambda_1`` is produced
at the lower end of the rope. The wavelength of
the pulse when it reaches the top of the rope is
``\lambda_2``. The ratio ``\lambda_2``/``\lambda_1`` is :
(1)``\sqrt\frac {m_1}{m_2}``
(2)``\sqrt\frac {m_1 + m_2}{m_2}``
(3)``\sqrt\frac {m_2}{m_1}``
(4)``\sqrt\frac {m_1 + m_2}{m_1}``

A refrigerator works between 4°C and 30°C. It is
required to remove 600 calories of heat every
second in order to keep the temperature of the
refrigerated space constant. The power required is:
(Take 1 cal = 4.2 Joules)
(1) 2.365 W
(2) 23.65 W
(3) 236.5 W
(4) 2365 W

An air column, closed at one end and open at the
other, resonates with a tuning fork when the
smallest length of the column is 50 cm. The next
larger length of the column resonating with the
same tuning fork is :
(1) 66.7 cm
(2) 100 cm
(3) 150 cm
(4) 200 cm

Consider the junction diode as ideal. The value of
current flowing through AB is :

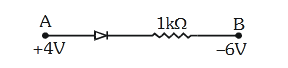
(1) 0 A
(2) ``10^{-2}`` A
(3) ``10^{-1}`` A
(4) ``10^{-3}`` A

The charge flowing through a resistance R varies
with time t as Q = at - ``bt^2``, where a and b are positive
constants. The total heat produced in R is:
(1)``\frac {a^3R}{6b}``
(2)``\frac {a^3R}{3b}``
(3) ``\frac {a^3R}{2b}``
(4)``\frac {a^3R}{b}``