HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
ICSE-X-Mathematics

Previous Year Paper year:2014

with Solutions - page 3
 
  • #5
  • #5-a [3]
    A shopkeeper bought a washing machine at a discount of 20% from a
    wholesaler, the printed price of the washing machine being Rs. 18,000. The
    shopkeeper sells it to a consumer at a discount of 10% on the printed price. If the rate
    of sales tax is 8%, find:
    Ans : Given: Printed price of washing machine = ``Rs.\ 18000``
    Rate of discount = ``20\% ``
  • #5-a-i
    the VAT paid by the shopkeeper.
    Ans : Amount of discount to shopkeeper = ``\frac{20}{100}\times 18000=Rs.\ 3600 ``
    Shopkeeper.s Price = ``18000-3600 = Rs.\ 14400 ``
    Sales Tax paid by shopkeeper = ``\frac{8}{100}\times 14400=Rs.\ 1152 ``
    Discount for consumer = ``\frac{10}{100}\times 18000=Rs.\ 1800 ``
    Price of consumer =``18000-1800= Rs.\ 16200 ``
    Tax charged by the shopkeeper = ``\frac{8}{100}\times 16200=Rs.\ 1296 ``
    Since, Tax paid by the shopkeeper = ``Rs.\ 1152 ``
    VAT paid by the shopkeeper=Tax charged . Tax Paid =``1296-1152=Rs.\ 144 ``
  • #5-a-ii
    the total amount that the consumer pays for the washing machine.
    Ans : Total amount paid by the consumer for washing machine = ``1620+1296 = Rs. \ 17496``
  • #5-b [3]
    If
    $$\frac{x^2 + y^2}{x^2 - y^2} = \frac{17}{8} $$
    then find the value of :
    Ans : Given: ``\frac{x^{2}+y^{2}}{x^{2}-y^{2}}=\frac{17}{8}``
  • #5-b-i
    x : y
    Ans : Applying componendo and dividend
    ``\frac{(x^{2}+y^{2}) +(x^{2}-y^{2})}{(x^{2}+y^{2})-(x^{2}-y^{2})}=\frac{17+8}{17-8} ``
    ``\Rightarrow \frac{2x^{2}}{2y^{2}}=\frac{25}{9}= \frac{x^{2}}{y^{2}}=\frac{25}{90}``
    ``\Rightarrow \frac{x}{y}=\frac{5}{3}``
    ``\Rightarrow x:y=5:3 ``
  • #5-b-ii
    $$\frac{x^3 + y^3}{x^3 - y^3} $$
    Ans : Cubing both sides we get
    ``\frac{x^{3}}{y^{3}}=\frac{5^{3}}{3^{3}}=\frac{125}{27}``
    Applying componendo and dividend
    ``\frac{x^{3}+y^{3}}{x^{3}-y^{3}}=\frac{125+27}{125-27}``
    ``\Rightarrow \frac{x^{3}+y^{3}}{x^{3}-y^{3}}=\frac{152}{98}``
    ``\Rightarrow \frac{x^{3}+y^{3}}{x^{3}-y^{3}}=\frac{76}{49}``
  • #5-c [4]
    In ``△ABC, ∠ABC = ∠DAC. AB = 8 cm, AC = 4 cm, AD = 5 cm.``

    i) Prove that â–³ ACD is similar to â–³ BCA.
    ii) Find BC and CD
    iii) Find area of â–³ACD : area of â–³BCA
    Ans :
    (i) In ``\triangle ACD`` and ``\triangle BCA``
    ``\angle C`` (common angle)

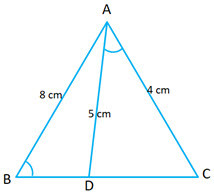
    ``\angle ABC = \angle CAD`` (given)
    Therefore ``\triangle ACD \sim \triangle BCA`` (AAA Postulate)
    (ii) Since ``\triangle ACD \sim \triangle BCA ``
    ``\Rightarrow \frac{AC}{BC}=\frac{CD}{CA}=\frac{AD}{BA}`` (corresponding sides are proportional)
    ``\frac{4}{BC}=\frac{CD}{4}=\frac{5}{8}``
    ``\Rightarrow \frac{4}{BC}=\frac{5}{8} \ and \ \frac{CD}{4}=\frac{5}{8}``
    ``\Rightarrow BC=\frac{4\times 8}{5}=\frac{32}{5}=6.4 \ cm`` and CD= `` \frac{5}{8}\times 4=\frac{5}{2}=2.5 \ cm``
    (iii) Since ``\Delta ACD \sim \Delta ABC``
    ``\frac{area \ (\Delta ACD)}{area \ (\Delta ABC)}=\frac{AC^{2}}{AB^{2}} = \frac{4^{2}}{8^{2}}=\frac{16}{64}=\frac{1}{4}``
    area ``\ (\Delta ACD ) \ : \ area \ (\Delta ABC)=1:4 ``
  • #6
  • #6-a [3]
    The value of 'a' for which of the following points A(a, 3), B (2, 1) and C(5, a) are
    collinear. Hence find the equation of the line.
    Ans : Given: A (a,3), B(2,1) and C(5,a) are collinear.
    ``Slope \ of \ AB= Slope \ of \ BC ``
    ``\frac{1-3}{2-a}=\frac{a-1}{5-1} ``
    ``\frac{-2}{2-a}=\frac{a-1}{3} ``
    ``\Rightarrow \ \ \ -6=(2-a)(a-1) ``
    ``\Rightarrow \ \ \ -6=2a-2-a^{2}+a ``
    ``\Rightarrow \ \ \ a^{2}-3a-4=0 ``
    ``\Rightarrow \ \ \ a^{2}-4a+a-4=0 ``
    ``\Rightarrow \ \ \ (a-4)(a+1)=0 ``
    ``a=4, -1 ``
    Rejecting a=-1
    ``Slope of BC = \frac{a-1}{5-2}=\frac{4-1}{3}=\frac{3}{3} =1``
    ``Equation \ of \ BC; (y-1)=1 (x-2) ``
    y-1=x-2
    x-y=1
  • #6-b [3]
    Salman invests a sum of money in Rs. 50 shares, paying 15% dividend quoted at 20%
    premium. If his annual dividend is Rs. 600, calculate:
    Ans : Nominal value of share = ``Rs. \ 50``
    Dividend on 1 share = ``\frac{15}{100}\times 50=Rs. \ 7.50``
    Total dividend of Salman =``Rs. \ 600``
  • #6-b-i
    the number of shares he bought.
    Ans : No. of shares Salman bought = ``\frac{600}{7.50}=80 ``
  • #6-b-ii
    his total investment.
    Ans : Premium on 1 share =``\frac{20}{100}\times 50=Rs. \ 10``
    Market value of 1 share = ``50+10=Rs. \ 60 ``
    Total investment for 80 shares = ``80 \times 60 = Rs. \ 4800``
  • #6-b-iii
    the rate of return on his investment.
    Ans : Rate of return= ``\frac{600}{4800}\times 100=12.5\% ``
  • #6-c [4]
    The surface area of a solid metallic sphere is 2464 ``cm^2``. It is melted and recast into
    solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
    Ans : (i) Let the radius sphere = ``r \ cm ``
    Surface area of sphere = ``4\pi r^{2}=2464 \ cm^{2}``
    ``r^{2}=\frac{2464}{4\pi } ``
    ``r^{2}=\frac{2464\times 7}{4\times 22}=196 ``
    ``r=14\ cm ``
next page