Previous Year Paper year:2014 : ICSE-X-Mathematics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

ICSE-X-Mathematics

Previous Year Paper year:2014

with Solutions - page 2

#3-b [3]
Using the Remainder and Factor Theorem, factorise the following polynomial:
$$x^3 + 10x^2 - 37x + 26 $$
Ans : Let ``f(x)=x^3+10x^2-37x+26 ``
Putting ``x =1`` , we get
``f(1)=1+10-37+26=0 ``
By factor theorem x-1 is actor of f(x)
``x-1 ) \overline {x^3+10x^2-37x+26} (x^2+11x-26 ``
``(-) \ \ \underline {x^3-x^2}
11x^2-37x+26 ``
``(-) \ \ \underline{11x^2-37x}
{ -26x+26} ``
``(-) \ \ \underline{ -26x+26} x ``
On dividing ``x^{3}+10x^{2}-37x+26`` by (x-1) , we get ``x^{2}+11x-26`` as the quotient and remainder = 0
Therefore the other factor of f(x) are the factor of ``x^{2}+11x-26 ``
Now, ``x^{2}+11x-26``
= ``x^{2}+13x-2x-26 ``
= ``x(x+13)-2(x+13)``
= ``(x+13)(x-2)``
Hence ``x^{3}+10x^{2}-37x+26=(x-1)(x-2)(x+13)``

#3-c [4]
In the figure given below, ABCD is a rectangle. AB = 14 cm, BC = 7 cm.
From the rectangle, a quarter circle BFEC and a semicircle DGE are removed.
Calculate the area of the remaining piece of the rectangle. (Take ``\\pi = \frac{22}{7}``)

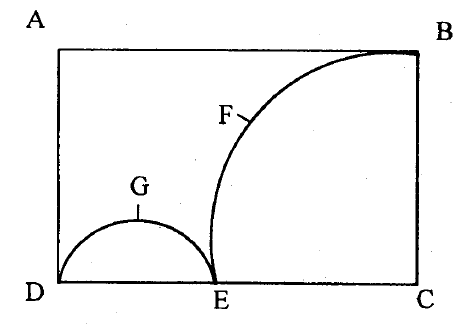Ans : Area of rectangle ABCD= ``14 \times 7 = 98cm ``
Area of quarter circle BFEC=``\frac{1}{4}\pi (7^{2})=\frac{49}{4}\pi``
Area of semicircle DGE= ``\frac{1}{2}\pi (\frac{7}{2})^2=\frac{1}{2}\times \frac{49}{4}\pi ``
Area of remaining piece of rectangle = ``98-[\frac{49}{4}\pi +\frac{1}{2}\times \frac{49}{4}\pi ]``
= ``98-\frac{49}{4}\pi \lbrack 1+\frac{1}{2}\rbrack ``
= ``98-\frac{49}{4}\times \frac{22}{7}\times \frac{3}{2}=98-\frac{231}{4}``
= ``98-57.75 = 40.25 cm^2 ``

#4

#4-a [3]
The numbers 6, 8, 10, 12, 13 and x are arranged in an ascending order.
If the mean of the observations is equal to the median, find the value of x.
Ans : Arrange numbers in ascending order are 6,8,10,12,13, x.
Mean = ``\frac{6+8+10+12+13+x}{6}=\frac{49+x}{6} ``
No. of terms (n) = ``6 \ (even) ``
Median = ``\frac{ (\frac{n}{2})^{th} \ term + (\frac{n}{2}+1)^{th} \ term }{2} ``
Median = ``\frac{ (\frac{6}{2})^{th} \ term + (\frac{6}{2}+1)^{th} \ term }{2} = \frac{3^{rd}+4^{th}}{2} = \frac{10+12}{2} = \frac{22}{2} = 11 ``
According to given condition
``\frac{49+x}{6}=11 \Rightarrow 49+x=66 ``
or x=17

#4-b [3]
In the figure, ∠DBC = 58°. BD is the diameter of the circle. Calculate:

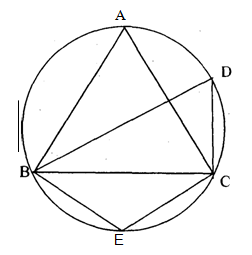Ans : In ``\triangle BCD , \angle DBC = 58° \ (given)``

#4-b-i
∠BDC
Ans : ``\angle BCD = 90°`` (angle in the semi circle)
``\therefore \angle DBC + \angle BCD + \angle BDC = 180° ``
``58°+90°+\angle BDC = 180°``
``\Rightarrow \angle BDC = 180°-148° = 32°``

#4-b-ii
∠BEC
Ans : ``\angle BEC + \angle BDC = 180° `` (cyclic quadrilateral)
``\angle BEC = 180°-32° = 148°``

#4-b-iii
∠BAC
Ans : ``\angle BAC = \angle BDC`` (angles in the same segment)
``\angle BAC = 32° ``

#4-c [4]
Use graph paper to answer the following questions. (Take 2 cm = 1 unit on both axes)
Ans : As shown in the graph below:

#4-c-i
Plot the points A(-4, 2) and B(2, 4)
Ans : Coordinate of A' = (4,2)

#4-c-ii
A' is the image of A when reflected at the y-axis. Plot it on the graph paper and write
the co-ordinates of A'.
Ans : Coordinate of B' = (2, 0)

#4-c-iii
B' is the image of B when reflected on the line AA'. Write the co-ordinates of B'.
Ans : Geometric name = kite

#4-c-iv
Write the geometric name of the figure ABA'B'.
Ans : AA' is the symmetric line.

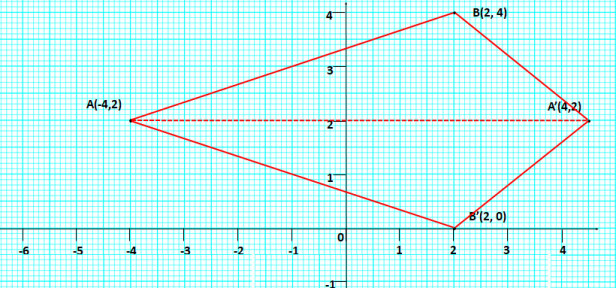
#4-c-v
Name a line of symmetry of the figure formed.

# [40]
Section : B
Attempt any four questions from this Section