HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
ICSE-X-Mathematics

Previous Year Paper year:2015

with Solutions - page 3
 
  • #5-a-iii
    Write the coordinates of B., C., D. and E..
    Ans : Coordinates : B', (-2, 5), C', (-5 ,2), D', (-5 , -2),E', (-2, -5)
  • #5-a-iv
    Name the figure formed by B C D E E. D. C. B..
    Ans : Octagon
  • #5-a-v [5]
    Name a line of symmetry for the figure formed.
    Ans : ``x-axis \ or \ y-axis ``.
  • #5-b [5]

    Virat opened a Savings Bank account in a bank on ``16^{th}`` April 2010. His pass book
    shows the following entries :

    Date Particulars Withdrawal (Rs.) Deposit (Rs.) Balance (Rs.)
    April 16, 2010 By cash - 2500 2500
    April 28th By cheque - 3000 5500
    May 9th To cheque 850 - 4650
    May 15th By cash - 1600 6250
    May 24th To cash 1000 - 5250
    June 4th To cash 500 - 4750
    June 30th To cheque - 2400 7150
    July 3rd By cash - 1800 8950


    Calculate the interest Virat earned at the end of 31st July, 2010 at 4% per annum
    interest. What sum of money will he receive if he closed the account on 1st August,
    2010?

    Ans :

    Qualifying principal for various months:

    Month Principal (Rs.)
    April 0
    May 4650
    June 4750
    July 8950
    Total = 18350
    P = ``Rs. \ 18350 \ R = 4\% \ and \ T= \frac{1}{12} ``
    I = ``P \times R \times T = 18350 \times \frac{4}{100} \times \frac{1}{12} = Rs. \ 61.16 ``
    Amount = ``8950+61.16= Rs. \ 9011.16 ``
    \\

  • #6
  • #6-a [3]
    If a, b, c are in continued proportion, prove that (a + b + c) (a . b + c) = a2 + b2 + c2.
    Ans : To prove: ``(a + b + c) (a - b + c) = a^2 + b^2 + c^2``
    Given ``a, b \ and\ c `` are in continued proportion
    Therefore ``\frac{a}{b} = \frac{b}{c} = k ``
    ``\Rightarrow a = bk \ and \ b = ck``
    This also implies ``a = (ck)k = ck^2``
    LHS ``= (a + b + c) (a - b + c) ``
    ``= (ck^2+ck+c)(ck^2-ck+c) ``
    ``= c^2(k^2+k+1)(k^2-k+1)``
    ``= c^2 \{ (k^2+1)+k \} \{ (k^2+1)-k \} ``
    ``=c^2 \{ (k^2+1)^2-k^2 \} ``
    ``= c^2 \{ k^4+1+2k^2-k^2 \} ``
    ``= c^2 \{ k^4+k^1+1 \} ``
    RHS ``= a^2 + b^2 + c^2 ``
    ``= (ck^2)^2+(ck)^2+c^2 ``
    ``= c^2k^4+c^2k^2+c^2 ``
    ``=c^2(k^4+k^2+1) ``
    Hence LHS = RHS
    Therefore Proved
  • #6-b
    In the given figure ABC is a triangle and BC is parallel to the y . axis. AB and AC intersect
    the y.axis at P and Q respectively.
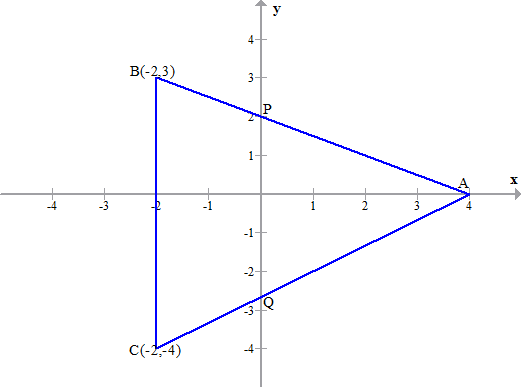    Ans : (i) Coordinates of A (4, 0)
  • #6-b-i
    Write the coordinates of A.
  • #6-b-ii
    Find the length of AB and AC.
    Ans : Coordinates of ``A (4, 0) \ and \ B (-2, 3)``
    Note: The distance between any two points ``(x_1, y_1) and (x_2, y_2) is = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} ``
    Length ``AB = \sqrt{(-2-4)^2+(3-0)^2} = \sqrt{36+9} = \sqrt{45} = 3 \sqrt{5} \ units ``
    Coordinates of ``A (4, 0) \ and \ C (-2, -4) ``
    Length ``AC = \sqrt{(-2-4)^2+(-4-0)^2} = \sqrt{36+16} = \sqrt{52} = 2 \sqrt{13} \ units ``
  • #6-b-iii
    Find the ratio in which Q divides AC.
    Ans : Let the required ratio be k:1
    Let the coordinate of`` P \ be \ (0, y)`` , since it lies on the y axis.
    Since ``x = \frac{kx_2+x_1}{k+1} ``
    ``\Rightarrow 0 = \frac{k \times (-2) +4}{k+1} ``
    ``\Rightarrow -2k+4=0 ``
    ``\Rightarrow k = 2 ``
    ``\Rightarrow m_1:m_2 = 2:1 ``
  • #6-b-iv [4]
    Find the equation of the line AC
    Ans : Equation of AC through Coordinates of ``A(4, 0) \ and \ C(-2, -4)``
    Required equation of the line: `` (y-y_1)=m(x-x_1) ``
    ``y-0= (\frac{0+4}{4+2}) (x-4) ``
    ``\Rightarrow 3y=2x-8 ``
    ``\Rightarrow \ or \ 3y-2x+8=0 ``
  • #6-c [3]
    Calculate the mean of the following distribution :
    Class Interval 0-10 10-20 20-30 30-40 40-50 50-60
    Frequency 8 5 12 35 24 16
    Ans :
    ClassMid Value x f fx
    0-105840
    10-2015575
    20-302512300
    30-4035351225
    40-5045241080
    50-605516880

    Total``\Sigma f=100 \Sigma fx=3600 ``
    Mean = ``\bar{x} = \frac{\mathcal{E}fx}{ \mathcal{E}f} = \frac{3600}{100} = 36 ``
    \\
  • #7
  • #7-a [3]
    Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8
    cm. Find the radius of the cone so formed.
    Ans : Volume of two spheres = Volume of cone
    ``\frac{4}{3}\pi \left(2^3\right)+\frac{4}{3}\pi \left(4^3\right)=\ \frac{1}{3}{\pi r}^2h
    32+256=r^2\times 8 ``
    ``r^2 = \frac{288}{8}``
    ``r^2 = 36 \Rightarrow r = 6 \ cm``
  • #7-b [3]
    Find 'a' of the two polynomials ``ax^3 + 3x^2 . 9`` and ``2x^3 + 4x + a``, leaves the same remainder
    when divided by x + 3.
    Ans : Let ``f(x) = {ax}^3+{3x}^2-9 \ and \ g(x) = {2x}^3+4x+a``
    Putting x = -3 in both the expressions
    ``f(-3) = {a(-3)}^3+{3(-3)}^2-9 ``
    ``g(-3) ={2(-3)}^3+4(-3)+a ``
    Given ``f(-3) = g(-3) ``
    Therefore ``{a(-3)}^3+{3(-3)}^2-9 = {2(-3)}^3+4(-3)+a ``
    ``-27a+27 -9 = -54-12+a ``
    ``27a+a = 27-9+54+12 ``
    ``28a=84 \Rightarrow a = 3 ``
next page