HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
ICSE-X-Mathematics

Previous Year Paper year:2015

with Solutions - page 2
 
  • #3
  • #3-a [3]
    In the given figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of
    the square. Two semicircles are drawn with AD and BC as diameters. Find the area
    of the shaded region.
    Take ``\left(\pi= \frac{22}{7}\right)``
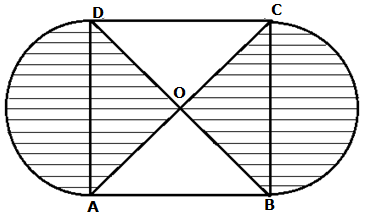    Ans : Given: Side ``=21\ cm ``
    Let Diagonal of the square = ``\sqrt{2} \times \ side``
    ``\therefore AC=BD=21\sqrt{2} ``
    ``\therefore AO=OC=BO=OD=\ \frac{21\sqrt{2}}{2} ``
    Area of ``\Delta AOD=Area\ of\ \Delta BOC=\ \frac{1}{2}\times \frac{21\sqrt{2}}{2}\times \frac{21\sqrt{2}}{2}=\frac{441}{4}{\ cm}^2 ``
    Area of semicircle ``= \frac{1}{2}\pi r^2 = \frac{1}{2}\times \frac{22}{7}\times \left(\frac{{21}^2}{2}\right)=\frac{693}{4}{\ cm}^2 ``
    Area of shaded region = Area of 2 semicircles + Area of \triangle AOD + \triangle BOC
    = ``2\ \times \frac{693}{4}+\frac{441}{4}+\frac{441}{4}+\frac{2268}{4} = 567\ {cm}^2 ``
  • #3-b [3]
    The marks obtained by 30 students in a class assignment of 5 marks are given
    below.
    Marks 0 1 2 3 4 5
    No. of Students 1 3 6 10 5 5

    Calculate the mean, median and mode of the above distribution.
    Ans : Below
    x f fx cf
    0101
    1334
    261210
    3103020
    452025
    552530

    ``\mathcal{E}f=30\ \ \ \ \ \ \ \mathcal{E}fx=90``
    Mean = ``\frac{\mathcal{E}fx}{\mathcal{E}f}=\frac{90}{30} = 3 ``
    Median = size ``\ of \left(\frac{N}{2}\right)th\ {obs}^n ``
    = size ``\ of \left(\frac{30}{2}\right)th\ {obs}^n ``
    = Size ``\ of 15 {}^{th} \ obs{}^{n} = 3 ``
    Mode = 3 marks (as highest frequency is 10)
  • #3-c [4]
    In the figure given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°,
    find the value of x, y and z.
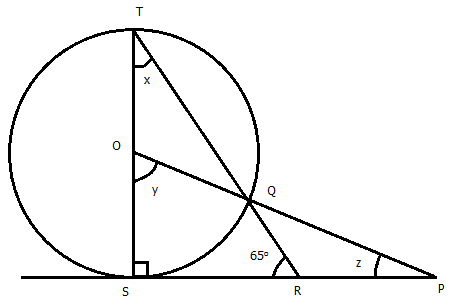    Ans : In ``\Delta OSP,\ \ \angle OSR=90{}^\circ`` (Radius is always perpendicular to the tangent)
    ``\ In\ \Delta TSR ``
    '
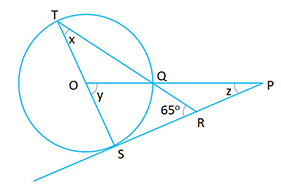    ``x+90{}^\circ +65{}^\circ =180{}^\circ ``
    ``x=25{}^\circ ``
    ``\angle SOQ=2\ \angle STR\ \ \left[Angle\ at\ centre=2\ \times angle\ at\ circumference \right]``
    ``y=2\times 25=50{}^\circ ``
    In ``\Delta OSP,\ \ 50{}^\circ +90{}^\circ +z=180{}^\circ``
    ``z=40{}^\circ ``
    \\
  • #4
  • #4-a
    Katrina opened a recurring deposit account with a Nationalised Bank for a period of 2
    years. If the bank pays interest at the rate 6% per annum and the monthly instalment is
    Rs. 1,000, find the:
    Ans : (i) Given ``P=Rs.1000,\ n=2\ years=\ 24\ months,\ r=6\%. ``
    ``I=P\times \frac{n(n+1)}{2}\times \frac{r}{12\times 100} ``
    ``= 1000\times \frac{24\ \left(24+1\right)}{2}\times \frac{6}{12\times 100} ``
    ``= 1000\times \frac{24\times 25}{2}\times \frac{6}{12\times 100}``
    =1500
  • #4-a-i
    Interest earned in 2 years.
  • #4-a-ii [3]
    Matured value
    Ans : Total money deposit in 24 months ``= Rs.\ 1000\times 24 = Rs. \ 24000``
    ``Matured\ Value=Total\ sum\ deposit+Interest =24000+1500 = Rs. \ 25500 ``
  • #4-b [3]
    Find the value of .K. for which x = 3 is a solution of the quadratic equation,
    $$(K + 2)x^2 . Kx + 6 = 0$$.
    Thus find the other root of the equation.
    Ans : ``\left(k+2\right)x^2-kx+6=0 ``
    ``Putting\ x=3 in given equation:``
    ``\left(k+2\right)\times 9-k\times 3+6=0 ``
    ``9k+18-3k+6=0 ``
    ``6k=-24 \Rightarrow k = -4 ``
    Putting k= -4 in given equation:
    ``-2x^2+4x+6=0``
    ``x^2-2x-3=0 ``
    ``x^2-3x+x-3=0 ``
    ``x\left(x-3\right)+1\left(x-3\right)=0 ``
    ``\left(x+1\right)\left(x-3\right)=0 ``
    ``x+1=0\ or\ x-3=0 ``
    ``x=-1\ or\ x=3 ``
    ``x=-1\ `` is the other root of the given equation.
  • #4-c [4]
    Construct a regular hexagon of side 5 cm. Construct a circle circumscribing the hexagon.
    All traces of construction must be clearly shown.
    Ans : Steps of Construction:
    '
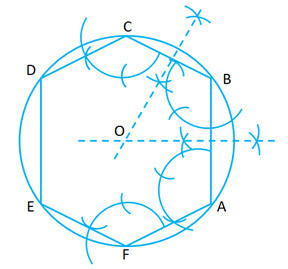    First draw a regular hexagon. The length of one side is 5 cm. You will get hexagon ABCDEF.
    Take any two adjacent sides and draw perpendicular bisectors.
    The point where these two bisectors intersect, is the center of the circle.
    With O as the center, draw a circle which will pass through all the vertices of the hexagon.
  • # [40]
    Section : B
    Attempt any four questions from this Section
  • #5
  • #5-a
    Use a graph paper for this question taking 1 cm = 1 unit along both the x and y
    axis :
    Ans : '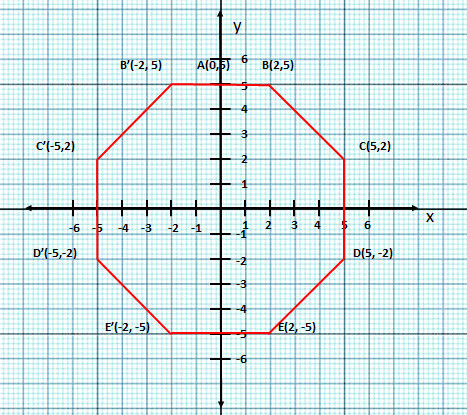
  • #5-a-i
    Plot the points A(0, 5), B(2, 5), C(5, 2), D(5, -2), E(2, -5) and F(0, -5).
    Ans : Shown in the diagram.
  • #5-a-ii
    Reflect the points B, C, D and E on the y-axis and name them respectively as B., C., D.
    and E..
    Ans : Shown in then diagram.
next page