HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
ICSE-X-Mathematics

Previous Year Paper year:2015

with Solutions -
 
  • #
    ICSE Board
    Class X Mathematics
    Board Question Paper . 2015
    (Two and a half hours)
    Answers to this Paper must be written on the paper provided separately.
    You will not be allowed to write during the first 15 minutes.
    This time is to be spent in reading the Question Paper.
    The time given at the head of this Paper is the time allowed for writing the answers.
    Attempt all questions from Section A and any four questions from Section B.
    All working, including rough work, must be clearly shown and must be done on the same
    sheet as the rest of the answer.
    Omission of essential working will result in loss of marks.
    The intended marks for questions or parts of questions are given in brackets [ ].
    Mathematical tables are provided.
  • # [40]
    Section : A
    Attempt all questions from this Section.
  • #1
  • #1-a
    A shopkeeper bought an article for Rs. 3,450. He marks the price of the article 16%
    above the cost price. The rate of sales tax charged on the article is 10%. Find the:
  • #1-a-i
    marked price of the article.
    Ans : Cost price of the article = Rs.3450
    Marked Price =``3450 + \frac{16}{100}\times 3450 = Rs. \ 4002 ``
  • #1-a-ii [3]
    price paid by a customer who buys the article.
    Ans : Price paid by the customer = ``Rs. 4002+\frac{10}{100}\times 4002 = Rs. \ 4402.20 ``
  • #1-b [3]
    Solve the following inequation and write the solution set:
    $$13x . 5 < 15x + 4 < 7x + 12, x \epsilon R $$
    Represent the solution on a real number line.
    Ans : Given
    ``13x-5<15x+4<7x+12 ``
    ``\Rightarrow 15x+4>13x-5\ \ and\ 15x+4<7x+12 ``
    ``\Rightarrow 15x-13x>-5-4 \ and \ 15x-7x<12-4 ``
    ``\Rightarrow 2x>-9 \ and \ 8x<8``
    ``\Rightarrow x>\frac{-9}{2} and x<1``
    Solution: ``\{ x: \frac{9}{2} < x< 1 , x \in R \} ``
    '
  • #1-c [4]
    Without using trigonometric tables evaluate:
    $$\frac{\sin65°}{\cos25°} + \frac{\cos32°}{\sin58°} - \sin28° \cdot \sec62°+ cosec^2 30°$$
    Ans : ``\frac{{\mathrm{sin\ } 65{}^\circ \ }}{{\mathrm{cos\ } 25{}^\circ \ }}+\frac{{\mathrm{cos} \ 32{}^\circ \ }}{{\mathrm{sin\ } 58{}^\circ \ }} -{\mathrm{sin} 28{}^\circ \ }.\ {\mathrm{sec \ } 62{}^\circ \ }+{\mathrm{cosec}^ 2 \ 30{}^\circ \ } ``
    ``= \frac{{\mathrm{cos} (90{}^\circ -65{}^\circ )\ }}{{\mathrm{cos\ } 25{}^\circ \ }}+\frac{{\mathrm{sin\ (} 90{}^\circ -32{}^\circ )\ }}{{\mathrm{sin\ } 58{}^\circ \ }} -{\mathrm{cos} (90{}^\circ -28{}^\circ )\times \frac{1}{{\mathrm{cos\ } 62{}^\circ \ }}+{(2)}^2\ } ``
    ``= \frac{{\mathrm{cos} 25{}^\circ \ }}{{\mathrm{cos} 25{}^\circ \ }}+\frac{{\mathrm{sin\ } 58{}^\circ \ }}{{\mathrm{sin} 58{}^\circ \ }} -{\mathrm{cos\ } 62{}^\circ \ }\times \frac{1}{cos\ 62{}^\circ }+4 ``
    ``= 1+1-1+4 = 5 ``
    \\
  • #2
  • #2-a [3]
    if A = \begin{bmatrix} 3 & x \\ 0 & 1 \\ \end{bmatrix} and B=
    \begin{bmatrix} 9 & 16 \\ 0 & -y \\ \end{bmatrix},
    find x and y where ``A^2``= B.
    Ans : ``A = \begin{bmatrix} 3 & x \\ 0 & 1 \end{bmatrix} and B = \begin{bmatrix} 9 & 16 \\ 0 & -7 \end{bmatrix}``
    ``A^2=B ``
    ``\begin{bmatrix} 3 & x \\ 0 & 1 \end{bmatrix} . \begin{bmatrix} 3 & x \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 9 & 16 \\ 0 & -y \end{bmatrix}``
    ``\begin{bmatrix} 3 \times 3 + x \times 0 & 3 \times x + x \times 1 \\ 0 \times 3 + 1 \times 0 & 0 \times x + 1 \times 1 \end{bmatrix} = \begin{bmatrix} 9 & 16 \\ 0 & -y \end{bmatrix}``
    ``\begin{bmatrix} 9 & 4x \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 9 & 16 \\ 0 & -y \end{bmatrix} ``
    Therefore ``4x = 16 \Rightarrow x = 4 ``
    And ``1 = -y \Rightarrow y = -1 ``
  • #2-b [3]
    The present population of a town is 2,00,000. The population is increased by 10% in
    the first year and 15% in the second year. Find the population of the town at the end
    of two years.
    Ans : Given: P =2,00,000
    Population after first year = ``200000\ [1+\frac{{10}}{100}] ^1 = 200000 \left[\frac{110}{100}\right]=220000``
    Principle for the second year = 220000
    Population at the end of second year = ``220000 \left[1+\frac{15}{100}\right] ``
    ``= 220000\times \frac{115}{100} = 253000 ``
  • #2-c
    Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and
    C(3, 2)
    Ans : '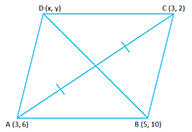
    Let the coordinate of ``D \ be \ (x,y)`` . In a parallelogram, the diagonals bisect each other.
    Mid point of AC =`` [\frac{3+3}{2},\ \frac{6+2}{2}] = (3,4) ``
    Mid point of BD = ``[\frac{x+5\ }{2},\ \frac{y+10}{2}] ``
  • #2-c-i
    the coordinate of the fourth vertex D
    Ans : `` 3=\frac{x+5}{2} \Rightarrow x = 1 ``
    ``4=\ \frac{y+10}{2} \Rightarrow y = -2 ``
    Coordinates of D (1, -2)
  • #2-c-ii
    length of diagonal BD
    Ans : BD = ``\sqrt{{(5-1}^2)+(10+{2)}^2} ``
    ``= \sqrt{16+144} = 4 \sqrt{10} \ units ``
  • #2-c-iii [4]
    equation of the side AD of the parallelogram ABCD
    Ans : Equation of AB:
    ``y-y_1 =\ \frac{y_{2-y_1}}{x_2-\ x_1} \left(x-x_1\right)``
    ``y-6= \ \frac{10-6}{5-3} \left(x-3\right)``
    ``y-6=\ \frac{4}{2}\left(x-3\right) ``
    ``y-6=2x-6 ``
    ``2x-y=0 ``
    \\
next page