HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
ICSE-X-Mathematics

Previous Year Paper year:2017

with Solutions -
 
  • #
    ICSE Board
    Class X Mathematics
    Board Question Paper 2017
    (Two and a half hours)
    Answers to this Paper must be written on the paper provided separately.
    You will not be allowed to write during the first 15 minutes.
    This time is to be spent in reading the Question Paper.
    The time given at the head of this Paper is the time allowed for writing the answers.
    Attempt all questions from Section A and any four questions from Section B.
    All working, including rough work, must be clearly shown and must be done on the same
    sheet as the rest of the answer.
    Omission of essential working will result in loss of marks.
    The intended marks for questions or parts of questions are given in brackets [ ].
    Mathematical tables are provided.
  • # [40]
    Section : A
    Attempt all questions from this Section.
  • #1
    Ans : Answers:
  • #1-a [3]
    If b is the mean proportion between a and c, show that
    $$\frac{a^4 + a^2b^2 + b^4}{b^4 + b^2c^2 + c^4} = \frac{a^2}{c^2}$$
    Ans : ``\frac{a^4+a^2b^2+b^4}{b^4+b^2c^2+c^4} = \frac{a^2}{c^2} ``
    Given ``\frac{a}{b} = \frac{b}{c} \Rightarrow b^2 = ac ``
    Now, LHS ``= \frac{a^4+a^2b^2+b^4}{b^4+b^2c^2+c^4} ``
    ``= \frac{a^4+a^2(ac)+(ac)^2}{(ac)^2+(ac)c^2+c^4}``
    ``= \frac{a^2(a^2+ac+c^2)}{c^2(a^2+ac+c^2)}``
    ``= \frac{a^2}{c^2} = RHS.``
    Hence Proved.
  • #1-b [3]
    Solve the equation ``4x^2 . 5x . 3 = 0 ``and give your answer correct to two decimal places.
    Ans : The equation is ``4x^2-5x-3=0 ``
    We know the roots of a quadratic equation are: ``x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} ``
    Here ``a = 4, b = -5 \ and \ c = -3 ``
    Substituting, we get
    ``x = \frac{5 \pm \sqrt{25+48}}{8}
    \Rightarrow x = \frac{5 \pm \sqrt{73}}{8}
    \Rightarrow x = \frac{5 \pm 8.54}{8}
    \Rightarrow x = \frac{5 + 8.54}{8}, \ \frac{5 - 8.54}{8}
    \Rightarrow x = \frac{13.54}{8}, \ \frac{-3.54}{8}
    \Rightarrow x = 1.69 \ or \ -0.44 ``
  • #1-c [4]
    AB and CD are two parallel chords of a circle such that AB = 24 cm and CD = 10 cm. If the
    radius of the circle is 13 cm. find the distance between the two chords.
    Ans : '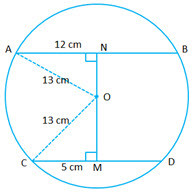
    ON ``= \sqrt{13^2-12^2} = \sqrt{25} = 5 \ cm ``
    OM = ``\sqrt{13^2-5^2} = \sqrt{144} = 12 \ cm ``
    MN = ``NO + OM = 5 + 12 = 17 \ cm ``
  • #2
    Ans : Answers:
  • #2-a [3]
    Evaluate without using trigonometric tables,
    $$\sin^2 28° + \sin^2 62° + \tan^2 38° -cot^2 52°+ \frac14 \sec^230° $$
    Ans : ``sin^2 \ 28 ° + sin^2 \ 62 ° +tan^2 \ 38 ° -cot^2 \ 52 ° + \frac{1}{4} sec^2 \ 30 ° ``
    ``= sin^2 \ 28 ° + sin^2 \ (90 ° - 28 ° )+tan^2 \ 38 ° -cot^2 \ (90 ° - 38 ° ) + \frac{1}{4} sec^2 \ 30 ° ``
    ``= sin^2 \ 28 ° + cos^2 \ 28 ° +tan^2 \ 38 ° -tan^2 \ 38 ° + \frac{1}{4} \times \frac{4}{3} ``
    ``= 1+ \frac{1}{3} ``
    ``= \frac{4}{3} ``
  • #2-b [3]
    If A = \begin{bmatrix} 1 & 3 \\ 3 & 4 \\ \end{bmatrix} and B=
    \begin{bmatrix}
    -2 & 1 \\
    -3 & 2 \\
    \end{bmatrix}and ``A^2 -5B^2 = 5C``. Find matrix C, where C is a 2 by 2 matrix.
    Ans : `` A^2 - 5B^2= 5C ``
    ``\Rightarrow \begin{bmatrix} 1 & 3 \ \ 3 & 4 \end{bmatrix} \times \begin{bmatrix} 1 & 3 \ \ 3 & 4 \end{bmatrix} - 5 \times \begin{bmatrix} -2 & 1 \ \ -3 & 2 \end{bmatrix} \times \begin{bmatrix} -2 & 1 \ \ -3 & 2 \end{bmatrix} = 5C ``
    ``\Rightarrow \begin{bmatrix} 1+9 & 3+12 \ \ 3+12 & 9+16 \end{bmatrix} - 5 \times \begin{bmatrix} 4-3 & -2+2 \ \ 6-6 & -3+4 \end{bmatrix} = 5C ``
    ``\Rightarrow \begin{bmatrix} 10 & 15 \ \ 15 & 25 \end{bmatrix} - 5 \times \begin{bmatrix} 1 & 0 \ \ 0 & 1 \end{bmatrix} = 5C ``
    ``\Rightarrow \begin{bmatrix} 5 & 15 \ \ 15 & 20 \end{bmatrix} = 5C ``
    ``\Rightarrow \begin{bmatrix} 1 & 3 \ \ 3 & 4 \end{bmatrix} = C ``
  • #2-c [4]
    Jaya borrowed Rs. 50,000 for 2 years. The rates of interest for two successive years are
    12% and 15% respectively. She repays 33,000 at the end of the first year. Find the amount
    she must pay at the end of the second year to clear her debt.
    Ans : We know`` A = P (1+ \frac{r}{100})^n ``
    A is the amount and P is the principal.
    For first year:
    ``P = 55000 \ Rs., r = 12 \%, n = 1 ``
    ``A = 55000 (1+ \frac{12}{100})^1 = 550 \times 112 = 56000 \ Rs ``
    For second year:
    ``P = (55000 - 33000) = 23000 \ Rs, r = 15 \%, n = 1 ``
    ``A = 23000 (1+ \frac{15}{100})^1 = 230 \times 115 = 26450 \ Rs``
  • #3
    Ans : Answers:
  • #3-a [3]
    The catalogue price of a computer set is Rs. 42,000. The shopkeeper gives a discount of
    10% on the listed price. He further gives an off-season discount of 5% on the discounted
    price. However, sales tax at 8% is charged on the remaining price after the two successive
    discounts. Find
    Ans : Cost Price = 42000 \ Rs.
    1st Discount = ``10 \% ``
    ``10 \% \ of \ 42000 Rs. = \frac{10}{100} \times 42000 = 4200 \ Rs. ``
    Price after discount = 42000 - 4200 = ``37800 \ Rs.``
    2nd Discount = ``5 \%``
    ``5 \% \ of \ 37800 \ Rs. = \frac{5}{100} \times 37800 = 1890 \ Rs. ``
    Price after discount = 37800 - 1890 = ``35910 \ Rs. ``
  • #3-a-i
    the amount of sales tax a customer has to pay
    Ans : Sales tax ``(@ 8 \%) = \frac{8}{100} \times 35910 = 2872.80 \ Rs ``
  • #3-a-ii
    the total price to be paid by the customer for the computer set.
    Ans : Price to be paid by the customer = 35910 + 2872.80 = ``38782.80 \ Rs. ``
  • #3-b [3]
    P(1, -2) is a point on the line segment A(3, -6) and B(x, y) such that AP : PB is equal to 2 : 3.
    Find the coordinates of B.
    Ans : A(3, -6), P(1, -2) and let B(x, y)
    m:n = 2:3
    We know the ratio formula: ``x = \frac{mx_2+nx_1}{m+n} , y = \frac{my_2+ny_1}{m+n}``
    Therefore
    ``1 = \frac{2x+3 \times 3}{2+3} ``
    ``\Rightarrow 5 = 2x+9 ``
    ``\Rightarrow x = -2 ``
    Similarly
    ``-2 = \frac{2y+3 \times (-6)}{2+3}``
    ``\Rightarrow -10 = 2y-18 ``
    ``\Rightarrow y = 4``
    Hence the coordinate of B(-2, 4)
next page