HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
ICSE-X-Mathematics

Previous Year Paper year:2018

with Solutions - page 4
 
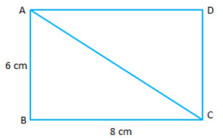
  • #7-b [3]
    On a map drawn to a scale of 1 : 50,000, a rectangular plot of land ABCD has the
    following dimensions. AB = 6 cm; BC = 8 cm and all angles are right angles. Find:
    Ans : Scale is 1:50000
    '
  • #7-b-i
    the actual length of the diagonal distance AC of the plot in km.
    Ans : ``AC = \sqrt{AB^2 +BC^2} = \sqrt{64+36} = \sqrt{100} = 10 \ cm``
    Let the length of AC be ``x`` on the ground
    Therefore ``\frac{1}{50000} = \frac{10}{x} \Rightarrow x = 500000 \ cm = 5 \ km``
  • #7-b-ii
    the actual area of the plot in sq. km.
    Ans : AB on the ground ``= 6 \times 50000 = 300000 \ cm = 3 \ km``
    BC on the ground ``= 8 \times 50000 = 400000 \ cm = 4 \ km``
    Therefore Area of ``ABCD = 3 \times 4 \ km^2 = 12 \ km^2``
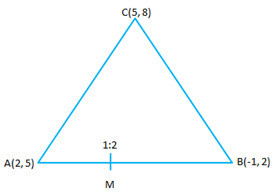
  • #7-c [4]
    A(2, 5), B(-1, 2) and C(5, 8) are the vertices of a triangle ABC, `M' is a point on AB
    such that AM : MB = 1 : 2. Find the co-ordinates of 'M’. Hence find the equation of the
    line passing through the points C and M.
    Ans : ``m_1 : m_2 = 1:2 \ and \ A(2,5), B(-1, 2) \ and \ C(5,8)``
    '
    Let M(x, y)
    ``x = \frac{m_1.x_2 + m_2.x_1}{m_1 + m_2} = \frac{1(-1) + 2(2)}{1+2} = \frac{3}{3} = 1``
    ``y = \frac{m_1.y_2 + m_2.y_1}{m_1 + m_2} = \frac{1(2) + 2(5)}{1+2} = \frac{12}{3} = 4``
    Hence M(1, 4)
    Slope of CM ``= \frac{y_2-y_1}{x_2-x_1} = \frac{8-4}{5-1} = \frac{4}{4} = 1``
    Therefore equation of CM
    ``y - y_1 = m(x- x_1)``
    ``\Rightarrow y - 4 = 1 (x- 1)``
    ``\Rightarrow y - x = 3``
  • #8
  • #8-a [3]
    Rs. 7500 were divided equally among a certain number of children. Had there been
    20 less children, each would have received Rs. 100 more. Find the original number
    of children.
    Ans : Let the number of children be ``= x``
    Therefore if ``x`` children received ``7500 \ Rs.``
    Then 1 child received ``\frac{7500}{x} \ Rs``.
    Let the number of children be = ``(x-20)``
    Therefore if ``(x-20)`` children received`` 7500 \ Rs.``
    Then 1 child received ``\frac{7500}{x-20} \ Rs.``
    Given ``\frac{7500}{x-20} - \frac{7500}{x} = 100``
    ``\Rightarrow \frac{75}{x-20} - \frac{75}{x} = 1``
    ``75x-7x(x-20) = (x-20)x``
    ``x^2 - 20x - 1500= 0``
    ``(x+30)(x-50)=0 \Rightarrow x = -30 \ (not possible) or \ 50``
    Therefore the number of children be = 50
  • #8-b [3]
    If the mean of the following distribution is 24, find the value of 'a '.
    Marks0-10 10-20 20-30 30-40 40-50
    Number of students7 a 8 10 5
    Ans : Marks Mid Term (\overline{x}) No. of Students (f) fx
    0-10 5 7 35
    10-20 15 a 15a
    20-30 25 8 200
    30-40 35 10 350
    40-50 45 5 225
    ``\Sigma f = 30+a \Sigma fx= 810+15a``
    ``Mean (\overline{x}) = \frac{\Sigma fx}{\Sigma f}``
    ``\Rightarrow 24 = \frac{810+15a}{30+a}``
    ``\Rightarrow 720 + 24a = 810 + 15a``
    ``\Rightarrow 9a = 90``
    ``\Rightarrow a = 10``
  • #8-c [4]
    Using ruler and compass only, construct a (triangle)triangle â–² ABC such that BC = 5 cm and AB = 6.5
    cm and ∠ABC = 120°
    Ans : '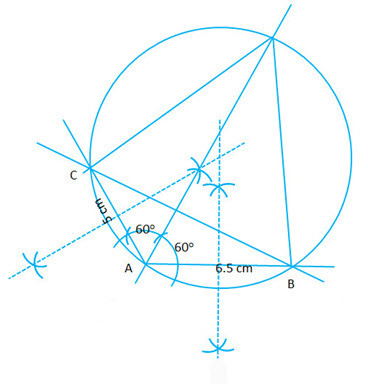
  • #8-c-i
    Construct a circum-circle of triangle â–²ABC
  • #8-c-ii
    Construct a cyclic quadrilateral ABCD, such that D is equidistant from AB and
    BC.
  • #9
  • #9-a [3]
    Priyanka has a recurring deposit account of Rs. 1000 per month at 10% per annum.
    If she gets Rs. 5550 as interest at the time of maturity, find the total time for which
    the account was held.
    Ans : Monthly Income ``(x) = 1000 \ Rs.``
    ``r= 10\%, \ \ \ I = 5550 Rs. \ \ \ Number \ of \ months = n``
    ``I = \frac{n(n+1)}{2} \times \frac{1}{12} \times x \times \frac{r}{100}``
    ``\Rightarrow 5550 = \frac{n(n+1)}{2} \times \frac{1}{12} \times 1000 \times \frac{10}{100}``
    ``\Rightarrow n(n+1) = \frac{5550 \times 2 \times 12}{100}``
    ``\Rightarrow n^2+n - 1332 = 0``
    ``\Rightarrow n^2 + 37n = 36n - 1332 = 0``
    ``\Rightarrow n(n+37)-36(n+37) = 0``
    ``\Rightarrow (n+37)(n-36) = 0``
    ``\Rightarrow n = -37 \ or \ 36 ``(negative number is not possible)
    Therefore n = 36
    Therefore total time line= 36 months or 3 years
  • #9-b
    In triangle â–²PQR, MN is parrallel to QR and
    ``\frac{\text{PM}}{\text{MQ}} = \frac23``
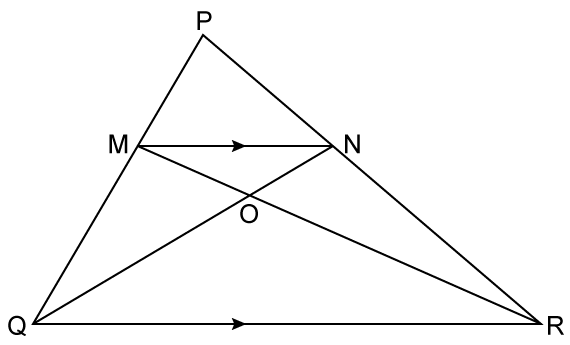    Ans : (i) In ``\triangle PMN \ and \ \triangle`` PQR
    '
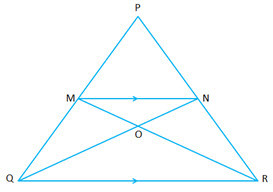    ``\angle P`` is common
    SInce MN ``\parallel`` QR
    ``\Rightarrow \angle PMN = \angle PQR and \angle PNM = \angle PRQ `` (alternate angles)
    Therefore ``\triangle PMN \sim \triangle PQR ``(by AAA Postulate)
    ``\Rightarrow \frac{PM}{PQ} = \frac{MN}{QR}``
    ``\Rightarrow \frac{PM}{PM+MQ} = \frac{MN}{QR} ``
    Given ``\frac{PM}{MQ} = \frac{2}{3} ``
    ``\Rightarrow \frac{2}{2+3} = \frac{MN}{QR} ``
    ``\Rightarrow \frac{MN}{QR} = \frac{2}{3} ``
  • #9-b-i
    Find
    ``\frac{MN}{QR}``
  • #9-b-ii
    Prove that triangle â–²OMN and triangle â–²ORQ are similar.
    Ans : Consider ``\triangle OMN`` & ``\triangle OQR``
    Since ``MN \parallel QR``
    ``\angle MNQ = \angle OQR ``(alternate angles)
    ``\angle NMO = \angle ORQ ``(alternate angles)
    Therefore ``\triangle OMN \sim \triangle OQR `` (AAA Postulate)
next page