NEET-XII-Physics
18: Geometrical Optics
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #Section : i
- Qstn #1Is the formula “Real depth/Apparent
depth=μvalid if viewed from a position quite away from the normal?Ans : No, because this formula is only valid when the angles of incidence and refraction are small. When the angles of incidence and refraction are large, we cannot use relations sini = tani and sinr = tanr to derive the formula for the apparent depth.
Page No 410:
- Qstn #2Can you ever have a situation in which a light ray goes undeviated through a prism?Ans : There is only one such situation. Light rays go undeviated through a prism only when the prism is kept in a medium that has the same refractive index as that of the prism itself. In all other situations, there will always be some minimum deviation in the path of a light ray passing through the prism.
Page No 410:
- Qstn #3Why does a diamond shine more than a glass piece cut to the same shape?Ans : A diamond shines more because of the phenomenon of total internal reflection (TIR). The refractive index of diamond is ≈2.4 and that of glass is ≈1.5.
By using the relation `` \mu =\frac{1}{\,\mathrm{\,sin\,}C}``, where C is the critical angle, we get refractive index (μ).
For a large refractive index, the value of the critical angle is small. Thus, for the diamond, the critical angle for total internal reflection is much smaller than that of the glass. Therefore, a great percentage of incident light gets internally reflected several times before it emerges out.
Page No 410:
- Qstn #4A narrow beam of light passes through a slab obliquely and is then received by an eye (figure 18-Q1). The index of refraction of the material in the slab fluctuates slowly with time. How will it appear to the eye? The twinkling of stars has a similar explanation.
Figure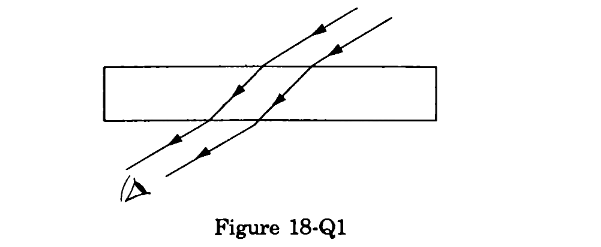
Ans : The beam of light will seem to appear and disappear, just like the twinkling of the stars. This is because the refractive index of the material in the slab fluctuates slowly with time. So, the light rays get refracted differently with time and this causes them to get concentrated during certain times, or get diffused at other times.
Page No 410:
- Qstn #5Can a plane mirror ever form a real image?Ans : No, a plane mirror can never form a real image. This is because in all possible situations of image formation, the light rays never actually meet after getting reflected, but they only appear to meet behind the mirror, forming a virtual image always.
Page No 410:
- Qstn #6If a piece of paper is placed at the position of a virtual image of a strong light source, will the paper burn after sufficient time? What happens if the image is real? What happens if the image is real but the source is virtual?Ans : No, the paper will not burn even after sufficient time. This is because the piece of paper is placed at the position of a virtual image of a strong light source, so light rays are not actually converging at that point, but seem to converge. As no light rays are concentrating on the point, the paper will never burn.
Instead, if the paper is placed at the position of a real image, it will burn as the light rays are actually concentrating on the point. Also, when we have the real image of a virtual source, it will also cause the burning of paper due to same reason; the light rays are actually meeting at the point.
Page No 410:
- Qstn #7Can a virtual image be photographed by a camera?Ans : Yes, a virtual image can be photographed by a camera. This is because the light rays emitting from a virtual image and reaching the lens of the camera are real. A virtual image is formed from a reflecting surface after reflection of real incident rays, so these rays enter the camera to provide effects on the photographic film. Just like a virtual image can be seen by us in a mirror with our eyes, it can be photographed by a camera.
Page No 410:
- Qstn #8In motor vehicles, a convex mirror is attached near the driver’s seat to give him the view of the traffic behind. What is the special function of this convex mirror which a plane mirror can not do?Ans : The special function of a convex mirror is that it creates the image of a distant object that is reduced in size, is upright or erect and always lies within the virtual focal length of the mirror. A plane mirror cannot do this. Also, as the image is formed within the focal length, the image is close to the mirror as well as is small in size, enabling the driver to clearly view the nearer vehicles behind the motor vehicle.
Page No 410:
- Qstn #9If an object far away from a convex mirror moves towards the mirror, the image also moves. Does it move faster, slower or at the same speed as compared to the object?Ans : The image of the object moves slower compared to the object. It can be explained using the mirror formula :`` \frac{1}{u}+\frac{1}{v}=\frac{1}{f}``
We know that for a convex mirror, the object distance (u) is positive, image distance (v) is negative and the focal length (d) is also negative. Thus mirror formula of a convex mirror is:`` \frac{1}{u}-\frac{1}{v}=-\frac{1}{f}``
As u = +ve
`` \frac{1}{v}-\frac{1}{f}>0``
`` \frac{1}{v}>\frac{1}{f}``
`` v<f``
Therefore, the image is always formed within the focal length of the mirror. Thus, the distance moved by the image is much slower than the distance moved by the object.
Page No 410:
- Qstn #10Suppose you are inside the water in a swimming pool near an edge. A friends is standing on the edge. Do you find your friend taller or shorter than his usual height?Ans : When viewed from the water, the friend will seem taller than his usual height.
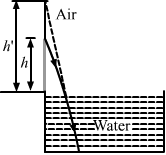
Let actual height be h and the apparent height be h'.
Here, the refraction is taking place from rarer to denser medium and a virtual image is formed.
Using
`` \frac{{\mu }_{1}}{-u}+\frac{{\mu }_{2}}{v}=\frac{{\mu }_{2}-{\mu }_{1}}{R}``
Where refractive index of water is μ2 and refractive index of air is μ1.
u and v are object and image distances, respectively.
R is the radius of curvature, here we will take it as ∞.
`` \frac{{\mu }_{1}}{-u}+\frac{{\mu }_{2}}{v}=\frac{{\mu }_{2}-{\mu }_{1}}{\infty }``
`` \frac{{\mu }_{1}}{u}=\frac{{\mu }_{2}}{v}``
`` v=\frac{{\mu }_{2}}{{\mu }_{1}}\times u``
As μ1 = 1
v = u × μ2
We know magnification is given by:
`` m=\frac{v}{u}``
Putting the value of v in the above equation:
`` m=\frac{u\times {\mu }_{2}}{u}``
`` m={\mu }_{2}``
`` ``
As the magnification is greater than 1, so the apparent height seems to be greater than actual height.
Page No 410:
- Qstn #11The equation of refraction at a spherical surface is
μ2ν-μ1μ=μ2-μ1R.
Taking
R=∞, show that this equation leads to the equation
Real depthApparent depth=μ2μ1for refraction at a plane surface.Ans : Proof:
`` \frac{{\mu }_{2}}{v}-\frac{{\mu }_{1}}{u}=\frac{{\mu }_{2}-{\mu }_{1}}{R}``
`` \,\mathrm{\,Now\,}R=\infty ``
`` \frac{{\mu }_{2}}{v}-\frac{{\mu }_{1}}{u}=\frac{{\mu }_{2}-{\mu }_{1}}{\infty }``
`` \frac{{\mu }_{2}}{v}-\frac{{\mu }_{1}}{u}=0``
`` \frac{{\mu }_{2}}{v}=\frac{{\mu }_{1}}{u}``
`` \frac{{\mu }_{1}}{{\mu }_{2}}=\frac{u}{v}``
`` \,\mathrm{\,But\,}\frac{u}{v}=\frac{\,\mathrm{\,Real\,}\,\mathrm{\,depth\,}/\,\mathrm{\,height\,}}{\,\mathrm{\,Apparent\,}\,\mathrm{\,depth\,}/\,\mathrm{\,height\,}}``
`` \therefore \frac{\,\mathrm{\,Real\,}\,\mathrm{\,depth\,}/\,\mathrm{\,height\,}}{\,\mathrm{\,Apparent\,}\,\mathrm{\,depth\,}/\,\mathrm{\,height\,}}=\frac{{\mu }_{\mathit{1}}}{{\mu }_{\mathit{2}}}``
Page No 410:
- Qstn #12μA thin converging lens is formed with one surface convex and the other plane. Does the position of image depend on whether the convex surface or the plane surface faces the object?Ans : Yes. Using the lens maker formula we can show it. We know that the formula is:
`` \frac{1}{f}=\left(\frac{{\mu }_{2}}{{\mu }_{1}}-1\right)\left(\frac{1}{{R}_{1}}-\frac{1}{{R}_{2}}\right)``
Where, f is the focal length of the thin converging lens.
μ2 and μ1 are refractive indexes of lens and air respectively.
R1 and R2 are the radius of curvature of convex and plane surfaces respectively.
Here, R2 = ∞ because of the plane surface.
Case 1
When the convex surface is facing the object, we have:
`` \frac{1}{f}=\left(\frac{{\mu }_{2}}{{\mu }_{1}}-1\right)\left(\frac{1}{{R}_{1}}-\frac{1}{\infty }\right)``
`` \frac{1}{f}=\left(\frac{{\mu }_{2}}{{\mu }_{1}}-1\right)\frac{1}{{R}_{1}}...\left(\,\mathrm{\,i\,}\right)``
Case 2
When the plane surface is facing the object, we have:
`` \frac{1}{f}=\left(\frac{{\mu }_{2}}{{\mu }_{1}}-1\right)\left(\frac{1}{\infty }-\frac{1}{{R}_{1}}\right)``
`` \frac{1}{f}=-\left(\frac{{\mu }_{2}}{{\mu }_{1}}-1\right)\frac{1}{{R}_{1}}...\left(\,\mathrm{\,ii\,}\right)``
For Case 1, the focal length is positive and for the Case 2 the focal length is negative. Thus, the image distance is different in both cases.
Page No 410:
- Qstn #13A single lens is mounted in a tube. A parallel beam enters the tube and emerges out of the tube as a divergent beam. Can you say with certainty that there is a diverging lens in the tube?Ans : Yes, we can say so with certainty, as only a diverging lens can cause a parallel beam of light to diverge.
Page No 410: