HomeLearn Fast select Course
Show Unit/ChapterChange UnitChange SubjectLast Menu
NEET-XII-Physics

17: Light Waves

with Solutions - page 7
Qstn# iv-28-a Prvs-QstnNext-Qstn
  • #28-a
    Show that in this case
    d=2λD/3. (b) Show that the intensity at P0 is three times the intensity due to any of the three slits individually.
    Figure
    Ans : Given:
    Wavelength of light = `` \lambda ``
    Path difference of wave fronts reaching from A and B is given by
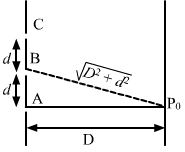
    `` ∆{x}_{B}={\,\mathrm{\,BP\,}}_{0}-{\,\mathrm{\,AP\,}}_{0}=\frac{\lambda }{3}``
    `` \Rightarrow \sqrt{{D}^{2}+{d}^{2}}-D=\frac{\lambda }{3}``
    `` \Rightarrow {D}^{2}+{d}^{2}={D}^{2}+\frac{{\lambda }^{2}}{9}+\frac{2\lambda D}{3}``
    We will neglect the term `` \frac{{\lambda }^{2}}{9}``, as it has a very small value.
    `` \therefore d=\sqrt{\frac{\left(2\lambda D\right)}{3}}`` (b) To calculating the intensity at P0, consider the interference of light waves coming from all the three slits.
    Path difference of the wave fronts reaching from A and C is given by
    `` {\,\mathrm{\,CP\,}}_{0}-{\,\mathrm{\,AP\,}}_{0}=\sqrt{{D}^{2}+{\left(2d\right)}^{2}}-D``
    `` =\sqrt{{D}^{2}+\frac{8\lambda D}{3}}-D\left(\,\mathrm{\,Using\,}\,\mathrm{\,the\,}\,\mathrm{\,value\,}\,\mathrm{\,of\,}d\,\mathrm{\,from\,}\,\mathrm{\,part\,}a\right)``
    `` =D{\left\{1+\frac{8\lambda }{3D}\right\}}^{\frac{1}{2}}-D``
    `` \,\mathrm{\,Expanding\,}\,\mathrm{\,the\,}\,\mathrm{\,value\,}\,\mathrm{\,using\,}\,\mathrm{\,binomial\,}\,\mathrm{\,theorem\,}\,\mathrm{\,and\,}\,\mathrm{\,neglecting\,}\text{the}\,\mathrm{\,higher\,}\,\mathrm{\,order\,}\,\mathrm{\,terms\,},\,\mathrm{\,we\,}\,\mathrm{\,get\,}:``
    `` D\left\{1+\frac{1}{2}\times \frac{8\lambda }{3D}+...\right\}-D``
    `` ``
    `` {\,\mathrm{\,CP\,}}_{0}-{\,\mathrm{\,AP\,}}_{0}=\frac{4\,\mathrm{\,\lambda \,}}{3}``
    So, the corresponding phase difference between the wave fronts from A and C is given by
    `` {\varphi }_{c}=\frac{2\pi ∆{x}_{C}}{\lambda }=\frac{2\pi \times 4\lambda }{3\lambda }``
    `` \Rightarrow {\varphi }_{c}=\frac{8\pi }{3}\,\mathrm{\,or\,}\left(2\pi +\frac{2\pi }{3}\right)``
    `` \Rightarrow {\varphi }_{c}=\frac{2\pi }{3}...\left(1\right)``
    `` \,\mathrm{\,Again\,},{\varphi }_{\,\mathrm{\,B\,}}=\frac{2\pi ∆{x}_{B}}{\lambda }``
    `` \Rightarrow {\varphi }_{\,\mathrm{\,B\,}}=\frac{2\pi \lambda }{3\lambda }=\frac{2\pi }{3}...\left(2\right)``
    So, it can be said that light from B and C are in the same phase, as they have the same phase difference with respect to A.
    Amplitude of wave reaching P0 is given by
    `` A=\sqrt{{\left(2a\right)}^{2}+{a}^{2}+2a\times a\,\mathrm{\,cos\,}\left(\frac{2\pi }{3}\right)}``
    `` =\sqrt{4{a}^{2}+{a}^{2}+2{a}^{2}\sqrt{3}}``
    `` \therefore {l}_{po}=\,\mathrm{\,K\,}{\left(\sqrt{3}r\right)}^{2}=3\,\mathrm{\,K\,}{r}^{2}=3l``
    Here, I is the intensity due to the individual slits and Ipo is the total intensity at P0.
    Thus, the resulting amplitude is three times the intensity due to the individual slits.

    Page No 382:
  • #28-b
    Show that the intensity at P0 is three times the intensity due to any of the three slits individually.
    Figure
    Ans : To calculating the intensity at P0, consider the interference of light waves coming from all the three slits.
    Path difference of the wave fronts reaching from A and C is given by
    `` {\,\mathrm{\,CP\,}}_{0}-{\,\mathrm{\,AP\,}}_{0}=\sqrt{{D}^{2}+{\left(2d\right)}^{2}}-D``
    `` =\sqrt{{D}^{2}+\frac{8\lambda D}{3}}-D\left(\,\mathrm{\,Using\,}\,\mathrm{\,the\,}\,\mathrm{\,value\,}\,\mathrm{\,of\,}d\,\mathrm{\,from\,}\,\mathrm{\,part\,}a\right)``
    `` =D{\left\{1+\frac{8\lambda }{3D}\right\}}^{\frac{1}{2}}-D``
    `` \,\mathrm{\,Expanding\,}\,\mathrm{\,the\,}\,\mathrm{\,value\,}\,\mathrm{\,using\,}\,\mathrm{\,binomial\,}\,\mathrm{\,theorem\,}\,\mathrm{\,and\,}\,\mathrm{\,neglecting\,}\text{the}\,\mathrm{\,higher\,}\,\mathrm{\,order\,}\,\mathrm{\,terms\,},\,\mathrm{\,we\,}\,\mathrm{\,get\,}:``
    `` D\left\{1+\frac{1}{2}\times \frac{8\lambda }{3D}+...\right\}-D``
    `` ``
    `` {\,\mathrm{\,CP\,}}_{0}-{\,\mathrm{\,AP\,}}_{0}=\frac{4\,\mathrm{\,\lambda \,}}{3}``
    So, the corresponding phase difference between the wave fronts from A and C is given by
    `` {\varphi }_{c}=\frac{2\pi ∆{x}_{C}}{\lambda }=\frac{2\pi \times 4\lambda }{3\lambda }``
    `` \Rightarrow {\varphi }_{c}=\frac{8\pi }{3}\,\mathrm{\,or\,}\left(2\pi +\frac{2\pi }{3}\right)``
    `` \Rightarrow {\varphi }_{c}=\frac{2\pi }{3}...\left(1\right)``
    `` \,\mathrm{\,Again\,},{\varphi }_{\,\mathrm{\,B\,}}=\frac{2\pi ∆{x}_{B}}{\lambda }``
    `` \Rightarrow {\varphi }_{\,\mathrm{\,B\,}}=\frac{2\pi \lambda }{3\lambda }=\frac{2\pi }{3}...\left(2\right)``
    So, it can be said that light from B and C are in the same phase, as they have the same phase difference with respect to A.
    Amplitude of wave reaching P0 is given by
    `` A=\sqrt{{\left(2a\right)}^{2}+{a}^{2}+2a\times a\,\mathrm{\,cos\,}\left(\frac{2\pi }{3}\right)}``
    `` =\sqrt{4{a}^{2}+{a}^{2}+2{a}^{2}\sqrt{3}}``
    `` \therefore {l}_{po}=\,\mathrm{\,K\,}{\left(\sqrt{3}r\right)}^{2}=3\,\mathrm{\,K\,}{r}^{2}=3l``
    Here, I is the intensity due to the individual slits and Ipo is the total intensity at P0.
    Thus, the resulting amplitude is three times the intensity due to the individual slits.

    Page No 382: