08: Work And Energy : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

08: Work and Energy

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #2
Two springs A and B(k_A = 2k_B) are stretched by applying forces of equal magnitudes a the four ends. If the energy stored in A is E, that in B is_A
(a) E/2
(b) 2E
(c) E
(d) E/4
digAnsr: b
Ans : (b) 2E
Let x_A and x_B be the extensions produced in springs A and B, respectively.
Restoring force on spring A, `` F={k}_{\,\mathrm{\,A\,}}{x}_{\,\mathrm{\,A\,}}`` ...(i)
Restoring force on spring B, `` F={k}_{\,\mathrm{\,B\,}}{x}_{\,\mathrm{\,B\,}}`` ...(ii)
From (i) and (ii), we get:
`` {k}_{\,\mathrm{\,A\,}}{x}_{\,\mathrm{\,A\,}}={k}_{\,\mathrm{\,B\,}}{x}_{\,\mathrm{\,B\,}}``
It is given that k_A = 2k_B
_{`` \therefore {x}_{\,\mathrm{\,B\,}}=2{x}_{\,\mathrm{\,A\,}}``}
Energy stored in spring A:
`` E=\frac{1}{2}{k}_{\,\mathrm{\,A\,}}{{x}_{\,\mathrm{\,A\,}}}^{2}`` ...(iii)
Energy stored in spring B:
`` E\text{'}=\frac{1}{2}{k}_{\,\mathrm{\,B\,}}{{x}_{\,\mathrm{\,B\,}}}^{2}=\frac{1}{2}\left(\frac{{k}_{\,\mathrm{\,A\,}}}{2}\right)(2{x}_{\,\mathrm{\,A\,}}{)}^{2}``
`` \therefore E\text{'}=2\times \left(\frac{1}{2}{k}_{\,\mathrm{\,A\,}}{{x}_{\,\mathrm{\,A\,}}}^{2}\right)=2E[\,\mathrm{\,From\,}(\,\mathrm{\,iii\,}\left)\right]``
Page No 131:

Qstn #3
Two equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is
(a)
12kx2(b)
-12kx2(c)
14kx2(d)
-14kx2
digAnsr: d
Ans : (d) `` -\frac{1}{4}k{x}^{2}``
The work done by the spring on both the masses is equal to the negative of the increase in the elastic potential energy of the spring.
The elastic potential energy of the spring is given by `` {E}_{p}=\frac{1}{2}k{x}^{2}``.
Work done by the spring on both the masses = `` -\frac{1}{2}k{x}^{2}``
∴ Work done by the spring on each mass = `` \frac{1}{2}\left(-\frac{1}{2}k{x}^{2}\right)=-\frac{1}{4}k{x}^{2}``

Page No 131:

Qstn #4
The negative of the work done by the conservative internal forces on a system equal the changes in
(a) total energy
(b) kinetic energy
(c) potential energy
(d) none of these.
digAnsr: c
Ans : (c) potential energy
The negative of the work done by the conservative internal forces on a system is equal to the changes in potential energy.
i.e. `` W=-∆P.E.``
Page No 131:

Qstn #5
The work done by the external forces on a system equals the change in
(a) total energy
(b) kinetic energy
(c) potential energy
(d) none of these
digAnsr: a
Ans : (a) total energy
When work is done by an external forces on a system, the total energy of the system will change.
Page No 131:

Qstn #6
The work done by all the forces (external and internal) on a system equals the change in
(a) total energy
(b) kinetic energy
(c) potential energy
(d) none of these
digAnsr: b
Ans : b in textbook, (a) total energy
The work done by all the forces (external and internal) on a system is equal to the change in the total energy.
Page No 131:

Qstn #7
____________ of a two particle system depends only on the separation between the two particles. The most appropriate choice for the blank space in the above sentence is
(a) Kinetic energy
(b) Total mechanical energy
(c) Potential energy
(d) Total energy.
digAnsr: c
Ans : (c) Potential energy
The potential energy of a two particle system depends only on the separation between the particles.
Page No 131:

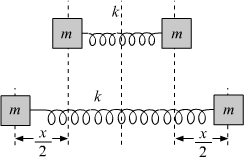
Qstn #8
A small block of mass m is kept on a rough inclined surface of inclination θ fixed in an elevator. the elevator goes up with a uniform velocity v and the block does not slide on the wedge. The work done by the force of friction on the block in time t will be
(a) zero
(b) mgvt cos²θ
(c) mgvt sin²θ
(d) mgvt sin 2θ
digAnsr: c
Ans : c.(c) mgvt sin²θ
Distance (d) travelled by the elevator in time t = vt
The block is not sliding on the wedge.
Then friction force (f) = mg sin`` \theta ``
Work done by the friction force on the block in time t is given by
`` W=Fd\,\mathrm{\,cos\,}(90-\theta )``
`` \Rightarrow W=mg\,\mathrm{\,sin\,}\theta \times d\times \,\mathrm{\,cos\,}(90-\theta )``
`` \Rightarrow W=mgd{\,\mathrm{\,sin\,}}^{2}\theta ``
`` \therefore W=mgvt{\,\mathrm{\,sin\,}}^{2}\theta ``

Page No 131:

Qstn #9
A block of mass m slides down a smooth vertical circular track. During the motion, the block is in
(a) vertical equilibrium
(b) horizontal equilibrium
(c) radial equilibrium
(d) none of these.
digAnsr: d
Ans : (d) none of these.
The net force on the block is not zero, therefore the block will not be in any given equilibrium.
Page No 131:

Qstn #10
A particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
(a)
gl(b)
2gl(c)
3gl(d)
5gl
digAnsr: c
Ans : (c) `` \sqrt{3gl}``
Suppose that one end of an extensible string is attached to a mass m, while the other end is fixed. The mass moves with a velocity v in a vertical circle of radius R. At some instant, the string makes an angle θ with the vertical as shown in the figure.

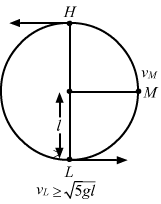
For a complete circle, the minimum velocity at L must be `` {v}_{\,\mathrm{\,L\,}}=\sqrt{5gl}``.
Applying the law of conservation of energy, we have:
Total energy at M = total energy at L
`` \,\mathrm{\,i\,}.\,\mathrm{\,e\,}.,\frac{1}{2}m{{v}_{\,\mathrm{\,M\,}}}^{2}+mgl=\frac{1}{2}m{{v}_{\,\mathrm{\,L\,}}}^{2}``
`` \Rightarrow \frac{1}{2}m{{v}_{\,\mathrm{\,M\,}}}^{2}=\frac{1}{2}m{{v}_{\,\mathrm{\,L\,}}}^{2}-mgl``
`` \,\mathrm{\,Using\,}{v}_{L}\ge \sqrt{5gl},\,\mathrm{\,we\,}\,\mathrm{\,have\,}:``
`` \frac{1}{2}m{{v}_{\,\mathrm{\,M\,}}}^{2}\ge \frac{1}{2}m\left(5gl\right)-mgl``
`` \therefore {v}_{\,\mathrm{\,M\,}}=\sqrt{3gl}``
Page No 131:

#
Section : iii

Qstn #1
A heavy stone is thrown in from a cliff of height h in a given direction. The speed with which it hits the ground
(a) must depend on the speed of projection
(b) must be larger than the speed of projection
(c) must be independent of the speed of projection
(d) may be smaller than the speed of projection.
digAnsr: a,b
Ans : (a) must depend on the speed of projection
(b) must be larger than the speed of projection
Consider that the stone is projected with initial speed v.
As the stone is falls under the gravitational force, which is a conservative force, the total energy of the stone remains the same at every point during its motion.
From the conservation of energy, we have:
Initial energy of the stone = final energy of the stone
`` \,\mathrm{\,i\,}.\,\mathrm{\,e\,}.,(K.E.{)}_{i}+(P.E.{)}_{i}=(K.E.{)}_{f}+(P.E.{)}_{f}``
`` \Rightarrow \frac{1}{2}m{v}^{2}+mgh=\frac{1}{2}m({v}_{max}{)}^{2}``
`` \Rightarrow {v}_{max}=\sqrt{{v}^{2}+2gh}``
`` ``
From the above expression, we can say that the maximum speed with which the stone hits the ground depends on the speed of projection and greater than it.
Page No 131:

Qstn #2
The total work done on a particle is equal to the change in its kinetic energy
(a) always
(b) only if the forces acting on it are conservative
(c) only if gravitational force alone acts on it
(d) only if elastic force alone acts on it.
digAnsr: a
Ans : (a) always
According to the work-energy theorem, the total work done on a particle is equal to the change in kinetic energy of the particle.
Page No 132:

Qstn #3
A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the plane. The motion of the particle takes place in a plane. It follows that
(a) its velocity is constant
(b) its acceleration is constant
(c) its kinetic energy is constant
(d) it moves in a circular path.
digAnsr: c,d
Ans : (c) its kinetic energy is constant
(d) it moves in a circular path.
When the force on a particle is always perpendicular to its velocity, the work done by the force on the particle is zero, as the angle between the force and velocity is 90`` °``. So, kinetic energy of the particle will remain constant. The force acting perpendicular to the velocity of the particle provides centripetal acceleration that causes the particle to move in a circular path.
Page No 132:

Qstn #4
Consider two observers moving with respect to each other at a speed v along a straight line. They observe a bock of mass m moving a distance l on a rough surface. The following quantities will be same as observed by the two observers.
(a) kinetic energy of the block at time t
(b) work done by friction
(c) total work done on the block
(d) acceleration of the block.
digAnsr: d
Ans : (d) acceleration of the block
Acceleration of the block will be the same to both the observers. The respective kinetic energies of the observers are different, because the block appears to be moving with different velocities to both the observers. Work done by the friction and the total work done on the block are also different to the observers.
Page No 132:

Qstn #5
You lift a suitcase from the floor and keep it on a table. The work done by you on the suitcase does not depend on
(a) the path taken by the suitcase
(b) the time taken by you in doing so
(c) the weight of the suitcase
(d) your weight
digAnsr: a,b,d
Ans : (a) the path taken by the suitcase
(b) the time taken by you in doing so
(d) your weight
Work done by us on the suitcase is equal to the change in potential energy of the suitcase.
i.e., W = mgh
Here, mg is the weight of the suitcase and h is height of the table.
Hence, work done by the conservative (gravitational) force does not depend on the path.
Page No 132: