HomeLearn Fast select Course
Show Unit/ChapterChange UnitChange SubjectLast Menu
NEET-XII-Physics

07: Circular Motion

with Solutions - page 6
Qstn# iv-29-a Prvs-QstnNext-Qstn
  • #29-a
    Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
    Figure
    Ans : Let us find the normal contact force (N) exerted by the plant of the block.
    `` \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}=0.1\times \frac{100}{50}=\frac{1}{5}=0.2`` (b) The plate is turned; so, the angle between the normal to the plate and the radius of the rod slowly increases.
    Therefore, we have:
    `` \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}\,\mathrm{\,cos\theta \,}...\left(\,\mathrm{\,i \,}\right)``
    `` \mu \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}\,\mathrm{\,sin\theta \,}...\left(ii\right)``
    `` \,\mathrm{\,On \,}\,\mathrm{\,using \,}\left(\,\mathrm{\,i \,}\right)\,\mathrm{\,and \,}\left(\,\mathrm{\,ii \,}\right),\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
    `` \frac{\mu m{v}^{2}}{r}\,\mathrm{\,cos \,}\theta =\frac{m{v}^{2}}{r}\,\mathrm{\,sin \,}\theta ``
    `` \Rightarrow \,\mathrm{\,\mu \,}=\,\mathrm{\,tan\theta \,}``
    `` \Rightarrow \,\mathrm{\,\theta \,}={\,\mathrm{\,tan \,}}^{-1}(0.58)\approx 30°``
    Page No 116:
  • #29-b
    The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
    Figure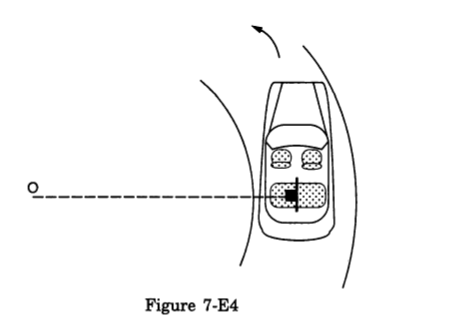
    Ans : The plate is turned; so, the angle between the normal to the plate and the radius of the rod slowly increases.
    Therefore, we have:
    `` \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}\,\mathrm{\,cos\theta \,}...\left(\,\mathrm{\,i \,}\right)``
    `` \mu \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}\,\mathrm{\,sin\theta \,}...\left(ii\right)``
    `` \,\mathrm{\,On \,}\,\mathrm{\,using \,}\left(\,\mathrm{\,i \,}\right)\,\mathrm{\,and \,}\left(\,\mathrm{\,ii \,}\right),\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
    `` \frac{\mu m{v}^{2}}{r}\,\mathrm{\,cos \,}\theta =\frac{m{v}^{2}}{r}\,\mathrm{\,sin \,}\theta ``
    `` \Rightarrow \,\mathrm{\,\mu \,}=\,\mathrm{\,tan\theta \,}``
    `` \Rightarrow \,\mathrm{\,\theta \,}={\,\mathrm{\,tan \,}}^{-1}(0.58)\approx 30°``
    Page No 116: