NEET-XII-Physics
07: Circular Motion
- #28A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R. A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
Figure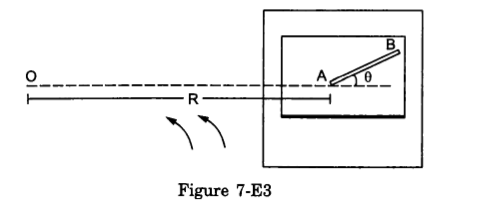 Ans : Let the mass of the particle be m.
Ans : Let the mass of the particle be m.
Radius of the path = R
Angular velocity = ω
Force experienced by the particle = mω2R
The component of force mRω2 along the line AB (making an angle with the radius) provides the necessary force to the particle to move along AB.
`` \therefore m{\omega }^{2}R\,\mathrm{\,cos \,}\theta =ma``
`` \Rightarrow a={\omega }^{2}R\,\mathrm{\,cos \,}\theta ``
`` ``
`` ``
Let the time taken by the particle to reach the point B be t.
`` \,\mathrm{\,On \,}\,\mathrm{\,using \,}\,\mathrm{\,equation \,}\,\mathrm{\,of \,}\,\mathrm{\,motion \,},\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` L=ut\mathit{+}\frac{\mathit{1}}{\mathit{2}}a{t}^{2}``
`` \Rightarrow L=\frac{1}{2}{\omega }^{2}R\,\mathrm{\,cos \,}\theta {t}^{2}``
`` \Rightarrow {t}^{\mathit{2}}=\frac{2L}{{\omega }^{2}R\,\mathrm{\,cos \,}\theta }``
`` \Rightarrow t=\sqrt{\frac{2L}{{\omega }^{2}R\,\mathrm{\,cos \,}\theta }}``
Page No 116: