NEET-XII-Physics
07: Circular Motion
- #14A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
(a) T1 > T2
(b) T2 > T1
(c) T1 = T2
(d) The relation between T1 and T2 depends on whether the rod rotates clockwise or anticlockwise.digAnsr: aAns : (a) T1 > T2
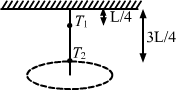
Let the angular velocity of the rod be `` \omega ``.
Distance of the centre of mass of portion of the rod on the right side of L/4 from the pivoted end:
`` {r}_{1}=\frac{L}{4}+\frac{1}{2}\left(\frac{3L}{4}\right)=\frac{5L}{8}``
Mass of the rod on the right side of L/4 from the pivoted end:
`` {m}_{1}=\frac{3}{4}M``
At point L/4, we have:
`` {T}_{1}={m}_{1}{\omega }^{2}{r}_{1}``
`` =\frac{3}{4}M{\omega }^{2}\frac{5}{8}L=\frac{15}{32}M{\omega }^{2}L``
Distance of the centre of mass of rod on the right side of 3L/4 from the pivoted end:
`` {r}_{1}=\frac{1}{2}\left(\frac{L}{4}\right)+\frac{3L}{4}=\frac{7L}{8}``
Mass of the rod on the right side of L/4 from the pivoted end:
`` {m}_{1}=\frac{1}{4}M``
At point 3L/4, we have:
`` {T}_{2}={m}_{2}{\omega }^{2}{r}_{2}``
`` =\frac{1}{4}M{\omega }^{2}\frac{7}{8}L=\frac{7}{32}M{\omega }^{2}L``
∴ T1 > T2
Page No 113: