HomeLearn Fast select Course
Show Unit/ChapterChange UnitChange SubjectLast Menu
NEET-XII-Physics

05: Newton's Laws of Motion

with Solutions - page 2
Qstn# ii-6 Prvs-QstnNext-Qstn
  • #6
    A block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally so that the block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude
    (a) mg
    (b) mg/cosθ
    (c) mg cosθ
    (d) mg tanθ
    digAnsr:   i
    Ans :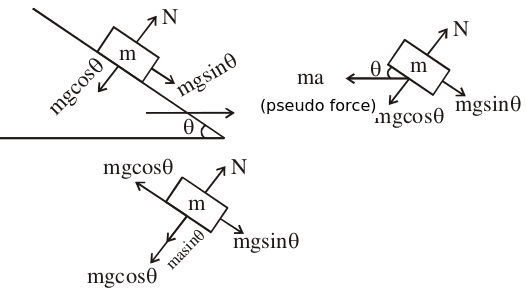 (b) mg/cosθ
    Free-body Diagram of the Small Block of Mass 'm'
    The block is at equilibrium w.r.t. to wedge. Therefore,
    mg sinθ = ma cosθ
    ⇒ a = gtanθ
    Normal reaction on the block is
    N = mg cosθ + ma sinθ
    Putting the value of a, we get:
    N = mg cosθ + mg tanθsinθ
    `` N=mg\,\mathrm{\,cos \,}\theta +mg\frac{\,\mathrm{\,sin \,}\theta }{\,\mathrm{\,cos \,}\theta }\,\mathrm{\,sin \,}\theta N=\frac{mg}{\,\mathrm{\,cos \,}\theta }``