NEET-XII-Physics
04: The Forces
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #3The sum of all electromagnetic forces between different particles of a system of charged particles is zero
(a) only if all the particles are positively charged
(b) only if all the particles are negatively charged
(c) only if half the particles are positively charged and half are negatively charged
(d) irrespective of the signs of the charges.digAnsr: dAns : (d) irrespective of the signs of the charges.
The sum of all electromagnetic forces between different particles of a system of charged particles is zero irrespective of the sign of the charges, because electromagnetic force is a vector quantity that depends upon the direction. So, we consider the directions while adding vector quantities.
- Qstn #4A 60 kg man pushes a 40 kg man by a force of 60 N. The 40 kg man has pushed the other man with a force of
(a) 40 N
(b) 0 N
(c) 60 N
(d) 20 NdigAnsr: cAns : (c) 60 N
According to Newton's third law, which states that an action-reaction pair of forces are equal in magnitude, the man who weighs 40 kg will push the other man with the same force of 60 N.
- #Section : iiiObjective II
- Qstn #1A neutron exerts a force on a proton which is
(a) gravitational
(b) electromagnetic
(c) nuclear
(d) weakdigAnsr: a,cAns : (a) gravitational
(c) nuclear
A neutron exerts both the gravitational and nuclear forces on a proton.
The gravitational force can be seen between a neutron and a proton. However, its strength is negligible. The nuclear force is exerted only if the interacting particles are neutrons or protons or both. A neutron cannot exert electromagnetic force, because it is a neutral particle.
- Qstn #2A proton exerts a force on a proton which is
(a) gravitational
(b) electromagnetic
(c) nuclear
(d) weakdigAnsr: a,b,cAns : (a) gravitational
(b) electromagnetic
(c) nuclear
A proton exerts gravitational, electromagnetic and nuclear forces on a proton.
The gravitational force can easily be seen everywhere; it the weakest among all the forces. It is negligible in elementary particles like protons.
The electromagnetic force can be seen between charged particles. Since proton is a charged particle, it can exert this force on other protons.
The nuclear force is present only if the interacting particles are protons or neutrons or both. So, this force can exist between two protons.
- Qstn #3Mark the correct statements:
(a) The nuclear force between two protons is always greater than the electromagnetic force between them.
(b) The electromagnetic force between two protons is always greater than the gravitational force between them.
(c) The gravitational force between two protons may be greater than the nuclear force between them.
(d) Electromagnetic force between two protons may be greater than the nuclear force acting between them.digAnsr: b,c,dAns : (b) The electromagnetic force between two protons is always greater than the gravitational force between them.
(c) The gravitational force between two protons may be greater than the nuclear force between them.
(d) Electromagnetic force between two protons may be greater than the nuclear force acting between them.
The electromagnetic force between two protons is always greater than the gravitational force between them, because gravitational force is the weakest force in nature.
We know that nuclear force is the strongest force in nature when the distance between two particles is less than `` {10}^{-14}\,\mathrm{\,m \,}``. However, the gravitational as well as electromagnetic forces between two protons may be greater than the nuclear force acting between them when the distance between them is more than `` {10}^{-14}\,\mathrm{\,m \,}``.
- Qstn #4If all matters were made of electrically neutral particles such as neutrons,
(a) there would be no force of friction
(b) there would be no tension in the string
(c) it would not be possible to sit on a chair
(d) the earth could not move around the sun.digAnsr: a,b,cAns : (a) there would be no force of friction
(b) there would be no tension in the string
(c) it would not be possible to sit on a chair
For the existence of friction between two bodies and tension in a string, electromagnetic force is needed. Electromagnetic force exists only between charged particles. For sitting on a chair, we need fractional force. A neutral particle can exert gravitational force on other neutral particles. So, even if all the matters were made up of electrically neutral particles, the earth will still move around the sun.
- Qstn #5Which of the following systems may be adequately described by classical physics?
(a) motion of a cricket ball
(b) motion of a dust particle
(c) a hydrogen atom
(d) a neutron changing to a proton.digAnsr: a,bAns : (a) motion of a cricket ball
(b) motion of a dust particle
Classical physics adequately describes the motion of a ball and the motion of dust particles. It also describes Newton's law of motion, Newton's law of gravitation, Laws of thermodynamics, Maxwell's electromagnetism and Lorentz force. Classical physics easily describes the system of heavenly bodies like the Sun, the Earth and the Moon. However, it is inadequate for describing systems of particles which have sizes much smaller than `` {10}^{-6}\,\mathrm{\,m \,}`` (e.g., atom, nuclei and other elementary particles).
- Qstn #6The two ends of a spring are displaced along the length of the spring. All displacement have equal magnitudes. In which case or cases the tension or compression in the spring will have a maximum magnitude?
(a) the right end is displaced towards right and the left end towards left
(b) both ends are displaced towards right
(c) both ends are displaced towards left
(d) the right end is displaced towards left and the left end towards right.digAnsr: a,dAns : (a) the right end is displaced towards right and the left end towards left
(d) the right end is displaced towards left and the left end towards right.
When the right end is displaced towards the right and the left end towards the left, then this is the case of tension (expansion) and the spring will have maximum displacement.
When the right end is displaced towards the left and the left end towards the right, then this is the case of compression and ,again, the spring will have maximum displacement.
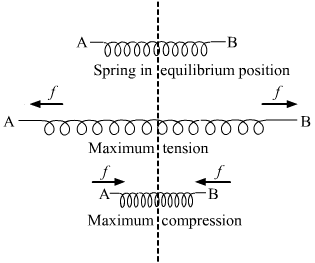
- Qstn #7Action and reaction
(a) act on two different objects
(b) have equal magnitude
(c) have opposite directions
(d) have resultant zero.digAnsr: a,b,c,dAns : (a) act on two different objects
(b) have equal magnitude
(c) have opposite directions
(d) have resultant zero.
The two forces `` \stackrel{\to }{F}\,\mathrm{\,and \,}-\stackrel{\to }{F}`` connected by Newton's third law are known as action-reaction pair.
For example, when a man jumps out from a ferry, he applied some force on the ferry. So, the action force in this case is the force applied by the man and the reaction is the force exerted by the ferry on the man. Both the forces act upon different objects (the man and the ferry) but have equal magnitudes and opposite directions. As a result, their resultant is zero.
- #Section : iv
- Qstn #1The gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67 × 10-17 N. Calculate the separation between the particles.Ans : Mass of the particle, m = 1 gm`` =\frac{1}{1000}\,\mathrm{\,kg \,}``
Let the distance between the two particles be r.
Gravitational force between the particle, F = 6.67 × 10-17 N
Also, `` \,\mathrm{\,F \,}=\frac{G{m}_{1}{m}_{2}}{{r}^{2}}``
Substituting the respective values in the above formula, we get:
`` 6.67\times {10}^{-17}=\frac{6.67\times {10}^{-11}\times \left(1/1000\right)\times \left(1/1000\right)}{{r}^{2}}``
`` \Rightarrow {r}^{2}=\frac{6.67\times {10}^{-6}\times {10}^{-11}}{6.67\times {10}^{-17}}``
`` =\frac{{10}^{-17}}{{10}^{-17}}=1``
`` \Rightarrow r=\sqrt{1}=1\,\mathrm{\,m \,}``
∴ The separation between the particles is 1 m.
- Qstn #2Calculate the force with which you attract the earth.Ans : Consider that a man is standing on the surface of the Earth.
Force acting on the man = mg
Here, m = mass of the man and g = acceleration due to gravity on the surface of earth (=10 m/s2)
Assume that the mass of the man is equal to 65 kg.
Then F = W = mg = 65 × 10 = 650 N = force acting on the man
∴ By Newton's third law (action-reaction are always equal), the man is also attracting the earth with a force of 650 N in the opposite direction.
- Qstn #3At what distance should two charges, each equal to 1 C, be placed so that the force between them equals your weight?Ans : Given: `` {q}_{1}={q}_{2}=1\,\mathrm{\,C \,}``
By Coulomb's law, the force of attraction between the two charges is given by
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\in }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` =\frac{9\times {10}^{9}\times 1\times 1}{{r}^{2}}``
However, the force of attraction is equal to the weight (F = mg).
`` \therefore mg=\frac{9\times {10}^{9}}{{r}^{2}}``
`` \Rightarrow {r}^{2}=\frac{9\times {10}^{9}}{m\times 10}=\frac{9\times {10}^{8}}{m}(\,\mathrm{\,Taking \,}g=10\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2})``
`` \Rightarrow {r}^{2}=\frac{9\times {10}^{8}}{m}``
`` \Rightarrow r=\frac{3\times {10}^{4}}{\sqrt{m}}``
Assuming that m = 81 kg, we have:
`` r=\frac{3\times {10}^{4}}{\sqrt{81}}``
`` =\frac{3}{9}\times {10}^{4}\,\mathrm{\,m \,}``
`` =3333.3\,\mathrm{\,m \,}``
∴ The distance r is 3333.3 m.
- Qstn #4Two spherical bodies, each of mass 50 kg, are placed at a separation of 20 cm. Equal charges are placed on the bodies and it is found that the force of Coulomb repulsion equals the gravitational attraction in magnitude. Find the magnitude of the charge placed on either body.Ans : Mass = 50 kg
Separation between the masses, r = 20 cm = 0.2 m
Let the change on each sphere be q.
Now, gravitational force, `` {F}_{\,\mathrm{\,G \,}}=G\frac{{m}_{1}{m}_{2}}{{r}^{2}}``
`` =\frac{67\times {10}^{-11}\times {\left(50\right)}^{2}}{{\left(0.2\right)}^{2}}``
`` =\frac{67\times {10}^{-11}\times 2500}{0.04}``
`` \,\mathrm{\,Coulomb \,}\,\mathrm{\,force \,},{F}_{\,\mathrm{\,c \,}}=\frac{1}{4\,\mathrm{\,\pi \,}{\in }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` =9\times {10}^{9}\frac{{q}^{2}}{0.04}``
Since FG = Fc, we have:
`` \frac{6.7\times {10}^{-11}\times 2500}{0.04}=\frac{9\times {10}^{9}\times {q}^{2}}{0.04}``
`` \Rightarrow {q}^{2}=\frac{6.7\times {10}^{-11}\times 2500}{9\times {10}^{9}}``
`` =\frac{9\times {10}^{9}}{0.04}=1809\times {10}^{-18}``
`` \therefore q=\sqrt{18.09\times {10}^{-18}}``
`` =4.3\times {10}^{-9}\,\mathrm{\,C \,}``
Thus, the charge of the spherical body is `` 4.3\times {10}^{-9}\,\mathrm{\,C \,}``.