NEET-XII-Physics
02: Physics and Mathematics
- #2Is it possible to add two vectors of unequal magnitudes and get zero? Is it possible to add three vectors of equal magnitudes and get zero?Ans : No, it is not possible to obtain zero by adding two vectors of unequal magnitudes.
Example: Let us add two vectors `` \stackrel{\to }{A}`` and `` \stackrel{\to }{B}`` of unequal magnitudes acting in opposite directions. The resultant vector is given by
`` R=\sqrt{{A}^{2}+{B}^{2}+2AB\mathrm{cos}\theta }
``
If two vectors are exactly opposite to each other, then
`` \theta =180°,\mathrm{cos}180°=-1
R=\sqrt{{A}^{2}+{B}^{2}-2AB}
\Rightarrow R=\sqrt{{\left(A-B\right)}^{2}}
\Rightarrow R=\left(A-B\right)\mathrm{or}\left(B-A\right)``
From the above equation, we can say that the resultant vector is zero (R = 0) when the magnitudes of the vectors `` \stackrel{\to }{A}`` and `` \stackrel{\to }{B}`` are equal (A = B) and both are acting in the opposite directions.
Yes, it is possible to add three vectors of equal magnitudes and get zero.
Lets take three vectors of equal magnitudes `` \stackrel{\to }{A,}\stackrel{\to }{B}\mathrm{and}\stackrel{\to }{C}``, given these three vectors make an angle of `` 120°`` with each other. Consider the figure below:
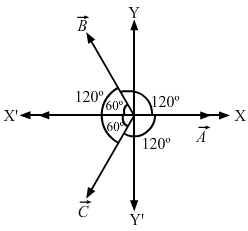
Lets examine the components of the three vectors.
`` {A}_{x}\mathit{=}A
{A}_{y}\mathit{=}0
{B}_{x}\mathit{=}\mathit{-}B\mathrm{cos}60°
{B}_{y}\mathit{=}B\mathrm{sin}\mathit{60}\mathit{°}
{C}_{x}\mathit{=}\mathit{-}C\mathrm{cos}60°
{C}_{y}\mathit{=}\mathit{-}C\mathrm{sin}60°
\mathrm{Here}\mathit{,}\mathit{}A\mathit{=}B\mathit{=}C
\mathrm{So},\mathrm{along}\mathrm{the}x-\mathrm{axis},\mathrm{we}\mathrm{have}:
A\mathit{-}\mathit{(}2A\mathrm{cos}60°\mathit{)}\mathit{=}\mathit{0}\mathit{,}\mathit{}as\mathit{}\mathrm{cos}\mathit{}60°\mathit{=}\frac{\mathit{1}}{\mathit{2}}\mathit{}
\Rightarrow B\mathrm{sin}60°\mathit{-}C\mathrm{sin}60°\mathit{=}\mathit{0}
``
Hence, proved.
Page No 27: