33: Thermal And Chemical Effects Of Electric Current : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

33: Thermal and Chemical Effects of Electric Current

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #4
A heater coil is to be constructed with a nichrome wire (ρ = 1.0 × 10^-6 Ωm) that can operate at 500 W when connected to a 250 V supply.

#4-a
What would be the resistance of the coil?
Ans : Let R be the resistance of the coil.
The power P consumed by a coil of resistance R when connected across a supply V is given by
`` P=\frac{{V}^{2}}{R}``
`` \Rightarrow R=\frac{{V}^{2}}{P}``
`` \Rightarrow R=\frac{{\left(250\right)}^{2}}{500}=125\,\mathrm{\,\Omega \,}``

#4-b
If the cross-sectional area of the wire is 0.5 mm², what length of the wire will be needed?
Ans : We know:
`` R=\,\mathrm{\,\rho \,}\frac{l}{A}``
`` \Rightarrow l=\frac{RA}{\,\mathrm{\,\rho \,}}``
`` \Rightarrow l=\frac{125\times 0.5\times {10}^{-6}}{{10}^{-6}}=62.5\,\mathrm{\,m\,}``

#4-c
If the radius of each turn is 4.0 mm, how many turns will be there in the coil?
Ans : Let n be the number of turns in the coil. Then,
`` l=2\,\mathrm{\,\pi \,}rn``
`` \mathit{\Rightarrow }n\mathit{=}\frac{\mathit{l}}{\mathit{2}\mathit{\pi }\mathit{r}}``
`` \mathit{\Rightarrow }n\mathit{=}\frac{\mathit{62}\mathit{.}\mathit{5}}{\mathit{2}\mathit{\times }\mathit{3}\mathit{.}\mathit{14}\mathit{\times }\mathit{4}\mathit{\times }{\mathit{10}}^{\mathit{-}\mathit{3}}}\mathit{\approx }2500``
Page No 219:

Qstn #5
A bulb with rating 250 V, 100 W is connected to a power supply of 220 V situated 10 m away using a copper wire of area of cross-section 5 mm². How much power will be consumed by the connecting wires? Resistivity of copper = 1.7 × 10^-8 Ωm
Ans : Let R be the resistance of the bulb. If P is the power consumed by the bulb when operated at voltage V, then
`` R=\frac{{V}^{2}}{P}=\frac{{\left(250\right)}^{2}}{100}=625\,\mathrm{\,\Omega \,}``
Resistance of the copper wire,
`` {R}_{\mathit{c}}=\,\mathrm{\,\rho \,}\frac{l}{\,\mathrm{\,A\,}}=\frac{1.7\times {10}^{-8}\times 10}{5\times {10}^{-6}}=0.034\,\mathrm{\,\Omega \,}``
The effective resistance,
`` {R}_{eff}=R+{R}_{c}=625.034\,\mathrm{\,\Omega \,}``
The current supplied by the power station,
`` i=\frac{\,\mathrm{\,V\,}}{{R}_{eff}}=\left\{\frac{220}{625.034}\right\}\,\mathrm{\,A\,}``
The power supplied to one side of the connecting wire,
`` P\text{'}={i}^{2}{R}_{c}``
`` ={\left(\frac{220}{625.034}\right)}^{2}\times 0.034``
The total power supplied on both sides,
`` 2P\text{'}={\left(\frac{220}{625.034}\right)}^{2}\times 0.034\times 2``
`` =0.0084\,\mathrm{\,W\,}=8.4\,\mathrm{\,mW\,}``
Page No 219:

Qstn #6
An electric bulb, when connected across a power supply of 220 V, consumes a power of 60 W. If the supply drops to 180 V, what will be the power consumed? If the supply is suddenly increased to 240 V, what will be the power consumed?
Ans : The resistance of a bulb that consumes power P and is operated at voltage V is given by
`` R=\frac{{V}^{2}}{P}=\frac{220\times 220}{60}=806.67\,\mathrm{\,\Omega \,}``
(a) Now the supply drops to V' = 180 V.
So, the power consumed,
`` P\text{'}=\frac{V{\mathit{\text{'}}}^{2}}{R}=\frac{{\left(180\right)}^{2}}{806.67}=40\,\mathrm{\,W\,}``
(b) Now the supply increases to V" = 240 V. Therefore,
`` P"=\frac{{{V}^{\mathit{\text{'}}\mathit{\text{'}}}}^{2}}{R}=71\,\mathrm{\,W\,}``
Page No 219:

Qstn #7
A servo voltage stabiliser restricts the voltage output to 220 V ± 1%. If an electric bulb rated at 220 V, 100 W is connected to it, what will be the minimum and maximum power consumed by it?
Ans : Output voltage, V = 220 V ± 1% = 220 V ± 2.2 V
The resistance of a bulb that is operated at voltage V and consumes power P is given by
`` R=\frac{{V}^{2}}{P}=\frac{(220{)}^{2}}{100}``
`` \Rightarrow R=\frac{48400}{100}=484\,\mathrm{\,\Omega \,}``
(a) For minimum power to be consumed, output voltage should be minimum. The minimum output voltage,
V' = (220 - 2.2) V
= 217.8 V
The current through the bulb,
`` i\text{'}=\frac{V\text{'}}{R}=\frac{217.8}{484}=0.45\,\mathrm{\,A\,}``
Power consumed by the bulb, P' = i' × V'
= 0.45 × 217.8 = 98.0 W
(b) For maximum power to be consumed, output voltage should be maximum. The maximum output voltage,
V" = (220 + 2.2) V
= 222.2 V
The current through the bulb,
`` i"=\frac{V"}{R}=\frac{222.2}{484}=0.459\,\mathrm{\,A\,}``
Power consumed by the bulb,
P" = i" × V"
= 0.459 × 222.2 = 102 W
Page No 219:

Qstn #8
An electric bulb marked 220 V, 100 W will get fused if it is made to consume 150 W or more. What voltage fluctuation will the bulb withstand?
Ans : Given that the operating voltage is V and power consumed is P.
Therefore, the resistance of the bulb,
`` R=\frac{{V}^{2}}{P}=\frac{(220\times 220)}{100}=484\,\mathrm{\,\Omega \,}``
`` ``
The power fluctuation, p = 150 W. So, the voltage fluctuation that the bulb can withstand,
`` v=\sqrt{pR}=\sqrt{150\times 484}``
`` =269.4\,\mathrm{\,V\,}=270\,\mathrm{\,V\,}``
The bulb will withstand up to 270 V.
Page No 219:

Qstn #9
An immersion heater rated 1000 W, 220 V is used to heat 0.01 m³ of water. Assuming that the power is supplied at 220 V and 60% of the power supplied is used to heat the water, how long will it take to increase the temperature of the water from 15°C to 40°C?
Ans : Given the operating voltage V and power consumed P, the resistance of the immersion heater,
`` R=\frac{{V}^{2}}{P}=\frac{{\left(220\right)}^{2}}{1000}=48.4\,\mathrm{\,\Omega \,}``
Mass of water, m = `` \frac{1}{100}`` × 1000 = 10 Kg
Specific heat of water, s = 4200 Jkg^{`` -``1} K^{`` -1``}
Rise in temperature, θ = 25°C
Heat required to raise the temperature of the given mass of water,
Q = msθ = 10 × 4200 × 25 = 1050000 J
Let t be the time taken to increase the temperature of water. The heat liberated is only 60%. So,
`` \left(\frac{{V}^{2}}{R}\right)`` × t × 60% = 1050000 J
`` \Rightarrow \frac{(220{)}^{2}}{48.4}\times t\times \frac{60}{100}=1050000``
⇒ t = 29.17 minutes
Page No 219:

Qstn #10
An electric kettle used to prepare tea, takes 2 minutes to boil 4 cups of water (1 cup contains 200 cc of water) if the room temperature is 25°C. (a) If the cost of power consumption is Re 1.00 per unit (1 unit = 1000 watt-hour), calculate the cost of boiling 4 cups of water. (b) What will be the corresponding cost if the room temperature drops to 5°C?
digAnsr: b
Ans : Time taken to boil 4 cups of water, t = 2 minutes
Volume of water boiled = 4 × 200 cc = 800 cc
Initial temperature, θ₁ = 25°C
Final temperature, θ₂ = 100°C
Change in temperature, θ = θ₂ - θ₁ = 75°C
Mass of water to be boiled, m = 800 × 1 = 800 gm = 0.8 Kg
Heat required for boiling water,
Q = msθ = 0.8 × 4200 × 75 = 252000 J
We know:
1000 watt - hour = 1000 × 3600 watt sec.
∴ Cost of boiling 4 cups of water`` =\frac{1}{1000\times 3600}\times 252000``
= Rs. 0.7
(b) Initial temperature, θ₁ = 5°C
Final temperature, θ₂ = 100°C
Change in temperature, θ = θ₂ - θ₁ = 95°C
Q = msθ = 0.8 × 4200 × 95 = 319200
∴ Cost of boiling 4 cups of water`` =\frac{1}{1000\times 3600}\times 319200``
= Rs 0.09
Page No 219:

Qstn #11
The coil of an electric bulb takes 40 watts to start glowing. If more than 40 W are supplied, 60% of the extra power is converted into light and the remaining into heat. The bulb consumes 100 W at 220 V. Find the percentage drop in the light intensity at a point if the supply voltage changes from 220 V to 200 V.
Ans : Case-I
: When the supply voltage is 220 V.
Power consumed by the bulb = 100 W
Excess power = 100 - 40 = 60 W
Power converted to light = 60% of 60 W = 36 W
Case-II
: When the supply voltage is 200 V.
Power consumed = `` \frac{200}{220}\times 100`` = 82.64 W
Excess power = 82.64 - 40 = 42.64 W
Power converted to light = 60% of 42.64 W = 25.584 W
Percentage drop in light intensity,
`` p=\frac{36-25.584}{36}\times 100``
`` \Rightarrow p=28.93\approx 29\%``
Page No 219:

Qstn #12
The 2.0 Ω resistor shown in the figure is dipped into a calorimeter containing water. The heat capacity of the calorimeter together with water is 2000 J K^-1.
Ans : The effective resistance of the circuit,
`` {\,\mathrm{\,R\,}}_{eff}=\left(\frac{6\times 2}{6+2}\right)+1=\frac{5}{2}\,\mathrm{\,A\,}``
`` ``
`` ``
Current i through the circuit,
`` i=\frac{V}{{R}_{eff}}=\frac{6}{5/2}=\frac{12}{5}\,\mathrm{\,A\,}``

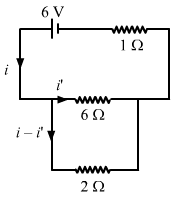
Let i' be the current through the 6 Ω resistor. Then,
i' × 6 = (i - i') × 2
`` \Rightarrow 6i\text{'}=\left(\frac{12}{5}\right)\times 2-2i\text{'}``
`` \Rightarrow 8i\text{'}=\frac{24}{5}``
`` \Rightarrow i\text{'}=\frac{24}{(5\times 8)}=\frac{3}{5}\,\mathrm{\,A\,}``
`` \Rightarrow i-i\text{'}=\frac{12}{5}-\frac{3}{5}=\frac{9}{5}\,\mathrm{\,A\,}``

#12-a
If the circuit is active for 15 minutes, what would be the rise in the temperature of the water?
Ans : Heat generated in the 2 Ω resistor,
H = (i - i')²Rt
`` \Rightarrow H=\left(\frac{9}{5}\right)\times \left(\frac{9}{5}\right)\times 2\times 15\times 60=5832\,\mathrm{\,J\,}``
The heat capacity of the calorimeter together with water is 2000 J K-1. Thus, 2000 J of heat raise the temp by 1 K.
∴ 5832 J of heat raises the temperature by `` \frac{5832}{2000}`` = 2.916 K

#12-b
Suppose the 6.0 Ω resistor gets burnt. What would be the rise in the temperature of the water in the next 15 minutes?
Figure
Ans : When the 6 Ω resistor gets burnt, the effective resistance of the circuit,
R_eff = 1 + 2 = 3 Ω
Current through the circuit,
i = `` \frac{6}{3}`` = 2 A
Heat generated in the 2 Ω resistor = (2)²× 2 × 15 × 60 = 7200 J
2000 J raise the temperature by 1 K.
∴ 7200 J raise the temperature by `` \frac{7200}{2000}`` = 3.6 K .
Page No 219:

Qstn #13
The temperatures of the junctions of a bismuth-silver thermocouple are maintained at 0°C and 0.001°C. Find the thermo-emf (Seebeck emf) developed. For bismuth-silver, a = - 46 × 10^-6 V°C^-1 and b = -0.48 × 10^-6 V°C^-2.
Ans : Given:
Difference in temperature, θ = 0.001°C,
a = - 46 × 10^-6 V °C^-1
b = - 0.48 × 10^-5 V °C^-2.
Emf, E = aθ + `` \frac{1}{2}``bθ²
⇒ E = (- 46 × 10^-6) × (0.001) `` -\frac{1}{2}`` × (0.48 × 10^-6 )× (0.001)²
= - 46 × 10^-9 - 0.24 × 10^-12
= - 46.0024 × 10^-9
= - 4.6 × 10^-8 V
Page No 219: