HomeLearn Fast select Course
Show Unit/ChapterChange UnitChange SubjectLast Menu
NEET-XII-Physics

32: Electric Current in Conductors

with Solutions - page 6
Qstn# iv-31 Prvs-QstnNext-Qstn
  • #31
    A wire of resistance 15.0 Ω is bent to form a regular hexagon ABCDEFA. Find the equivalent resistance of the loop between the points (a) A and B (b) A and C and (c) A and D.
    Ans : (a)
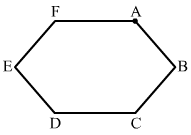
    From the figure, it can be seen that between points A and B, the resistance of the first side of the hexagon will be in parallel with the total resistance of the other five sides.
    The resistance of the first side can be calculated as shown below.
    Resistance of the first leg=`` \frac{\text{L}\,\mathrm{\,ength\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,that\,}\,\mathrm{\,portion\,}}{\text{T}\,\mathrm{\,otal\,}\,\mathrm{\,length\,}}\times R=\frac{{\displaystyle \frac{1}{6}}}{{\displaystyle \frac{5}{6}}+{\displaystyle \frac{1}{6}}}\times 15=15\times \frac{1}{6}``
    Total resistance of the 5 legs=`` \frac{{\displaystyle \frac{5}{6}}}{{\displaystyle \frac{1}{6}}+{\displaystyle \frac{5}{6}}}\times 15=\frac{5}{6}\times 15``
    ∴ The effective resistance between the points A and B,
    `` {R}_{\,\mathrm{\,eff\,}}=\frac{{\displaystyle \frac{15\times 5}{6}}\times {\displaystyle \frac{15}{6}}}{{\displaystyle \frac{15\times 5}{6}}+{\displaystyle \frac{15}{6}}}=\frac{{\displaystyle \frac{15\times 5\times 15}{6\times 6}}}{{\displaystyle \frac{75+15}{6}}}``
    `` =\frac{15\times 5\times 15}{6\times 90}=\frac{25}{12}``
    `` =2.08\,\mathrm{\,\Omega \,}`` (b) From the figure, it can be seen that between points A and C, the resistance of the first two sides of the hexagon will be in parallel with the total resistance of the other four sides.
    Resistance of the two legs =`` \frac{\text{L}\,\mathrm{\,ength\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,that\,}\,\mathrm{\,portion\,}}{\text{T}\,\mathrm{\,otal\,}\,\mathrm{\,length\,}}\times R=\frac{{\displaystyle \frac{2}{6}}}{{\displaystyle \frac{4}{6}}+{\displaystyle \frac{2}{6}}}\times 15=15\times \frac{2}{6}``
    Total resistance of the four legs=`` \frac{{\displaystyle \frac{4}{6}}}{{\displaystyle \frac{2}{6}}+{\displaystyle \frac{4}{6}}}\times 15=\frac{4}{6}\times 15``
    ∴ The effective resistance between the points A and C,
    `` {\,\mathrm{\,R\,}}_{eff}=\frac{{\displaystyle \frac{15\times 4}{6}}\times {\displaystyle \frac{15\times 2}{6}}}{{\displaystyle \frac{15\times 4}{6}}+{\displaystyle \frac{15\times 2}{6}}}=\frac{{\displaystyle \frac{15\times 4\times 2\times 15}{6\times 6}}}{{\displaystyle \frac{60+30}{6}}}``
    `` =\frac{15\times 2\times 4\times 15}{6\times 90}``
    `` =\frac{10}{3}=3.33\,\mathrm{\,\Omega \,}`` (c) From the figure, it can be seen that between points A and D, the resistance of the first three sides of the hexagon will be in parallel with the total resistance of the other three sides.
    Resistance of the three legs = `` \frac{\text{L}\,\mathrm{\,ength\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,that\,}\,\mathrm{\,portion\,}}{\text{T}\,\mathrm{\,otal\,}\,\mathrm{\,length\,}}\times R=\frac{{\displaystyle \frac{3}{6}}}{{\displaystyle \frac{3}{6}}+{\displaystyle \frac{3}{6}}}\times 15=15\times \frac{3}{6}``
    ∴ The effective resistance between the points A and D,
    `` {\,\mathrm{\,R\,}}_{\,\mathrm{\,eff\,}}=\frac{{\displaystyle \frac{15\times 3}{6}}\times {\displaystyle \frac{15\times 3}{6}}}{{\displaystyle \frac{15\times 3}{6}}+{\displaystyle \frac{15\times 3}{6}}}=\frac{{\displaystyle \frac{15\times 3\times 3\times 15}{6\times 6}}}{{\displaystyle \frac{90}{6}}}``
    `` =\frac{15\times 3\times 3\times 15}{6\times 90}=\frac{15}{4}=3.75\,\mathrm{\,\Omega \,}``
    Page No 199:
  • #31-a
    A and B
    Ans :
    From the figure, it can be seen that between points A and B, the resistance of the first side of the hexagon will be in parallel with the total resistance of the other five sides.
    The resistance of the first side can be calculated as shown below.
    Resistance of the first leg=`` \frac{\text{L}\,\mathrm{\,ength\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,that\,}\,\mathrm{\,portion\,}}{\text{T}\,\mathrm{\,otal\,}\,\mathrm{\,length\,}}\times R=\frac{{\displaystyle \frac{1}{6}}}{{\displaystyle \frac{5}{6}}+{\displaystyle \frac{1}{6}}}\times 15=15\times \frac{1}{6}``
    Total resistance of the 5 legs=`` \frac{{\displaystyle \frac{5}{6}}}{{\displaystyle \frac{1}{6}}+{\displaystyle \frac{5}{6}}}\times 15=\frac{5}{6}\times 15``
    ∴ The effective resistance between the points A and B,
    `` {R}_{\,\mathrm{\,eff\,}}=\frac{{\displaystyle \frac{15\times 5}{6}}\times {\displaystyle \frac{15}{6}}}{{\displaystyle \frac{15\times 5}{6}}+{\displaystyle \frac{15}{6}}}=\frac{{\displaystyle \frac{15\times 5\times 15}{6\times 6}}}{{\displaystyle \frac{75+15}{6}}}``
    `` =\frac{15\times 5\times 15}{6\times 90}=\frac{25}{12}``
    `` =2.08\,\mathrm{\,\Omega \,}``
  • #31-b
    A and C and
    Ans : From the figure, it can be seen that between points A and C, the resistance of the first two sides of the hexagon will be in parallel with the total resistance of the other four sides.
    Resistance of the two legs =`` \frac{\text{L}\,\mathrm{\,ength\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,that\,}\,\mathrm{\,portion\,}}{\text{T}\,\mathrm{\,otal\,}\,\mathrm{\,length\,}}\times R=\frac{{\displaystyle \frac{2}{6}}}{{\displaystyle \frac{4}{6}}+{\displaystyle \frac{2}{6}}}\times 15=15\times \frac{2}{6}``
    Total resistance of the four legs=`` \frac{{\displaystyle \frac{4}{6}}}{{\displaystyle \frac{2}{6}}+{\displaystyle \frac{4}{6}}}\times 15=\frac{4}{6}\times 15``
    ∴ The effective resistance between the points A and C,
    `` {\,\mathrm{\,R\,}}_{eff}=\frac{{\displaystyle \frac{15\times 4}{6}}\times {\displaystyle \frac{15\times 2}{6}}}{{\displaystyle \frac{15\times 4}{6}}+{\displaystyle \frac{15\times 2}{6}}}=\frac{{\displaystyle \frac{15\times 4\times 2\times 15}{6\times 6}}}{{\displaystyle \frac{60+30}{6}}}``
    `` =\frac{15\times 2\times 4\times 15}{6\times 90}``
    `` =\frac{10}{3}=3.33\,\mathrm{\,\Omega \,}``
  • #31-c
    A and D.
    Ans : From the figure, it can be seen that between points A and D, the resistance of the first three sides of the hexagon will be in parallel with the total resistance of the other three sides.
    Resistance of the three legs = `` \frac{\text{L}\,\mathrm{\,ength\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,that\,}\,\mathrm{\,portion\,}}{\text{T}\,\mathrm{\,otal\,}\,\mathrm{\,length\,}}\times R=\frac{{\displaystyle \frac{3}{6}}}{{\displaystyle \frac{3}{6}}+{\displaystyle \frac{3}{6}}}\times 15=15\times \frac{3}{6}``
    ∴ The effective resistance between the points A and D,
    `` {\,\mathrm{\,R\,}}_{\,\mathrm{\,eff\,}}=\frac{{\displaystyle \frac{15\times 3}{6}}\times {\displaystyle \frac{15\times 3}{6}}}{{\displaystyle \frac{15\times 3}{6}}+{\displaystyle \frac{15\times 3}{6}}}=\frac{{\displaystyle \frac{15\times 3\times 3\times 15}{6\times 6}}}{{\displaystyle \frac{90}{6}}}``
    `` =\frac{15\times 3\times 3\times 15}{6\times 90}=\frac{15}{4}=3.75\,\mathrm{\,\Omega \,}``
    Page No 199: